Scipy 插值

scipy.interpolate是插值模块，插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。我们可以认为插值是在一条直线或一条曲线上的两个点之间找到一个值的过程。这种插值工具不仅在统计中很有用，而且在科学、商业或需要预测落在两个现有数据点内的值时也很有用。

让我们创建一些数据，看看如何使用 scipy.interpolate 库来完成这种插值过程。

import numpy as np
from scipy import interpolate
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print(x,y)

运行示例

程序运行结果如下

[0.         0.36363636 0.72727273 1.09090909 1.45454545 1.81818182
 2.18181818 2.54545455 2.90909091 3.27272727 3.63636364 4.        ] 
[-0.65364362 -0.61966189 -0.51077021 -0.31047698 -0.00715476  0.37976236
  0.76715099  0.99239518  0.85886263  0.27994201 -0.52586509 -0.99582185]

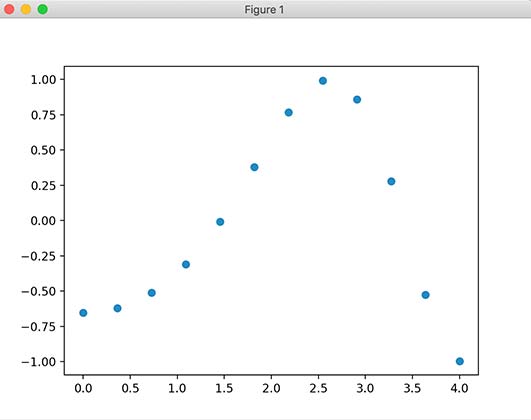
现在，我们有两个数组，x和y。假设这两个数组是空间中点的二维，让我们使用以下程序绘制并查看它们的图形界面。

import matplotlib.pyplot as plt

plt.plot(x, y,’o’)
plt.show()

程序运行结果如下

一维插值

scipy.interpolate 中的 interp1d 方法是一种基于固定数据点创建函数的便捷方法，可以使用线性插值在给定数据定义的域内的任何位置对其进行评估。

通过使用上面的数据，让我们创建一个插值函数并绘制一个新的插值图。

f1 = interp1d(x, y,kind = 'linear')

f2 = interp1d(x, y, kind = 'cubic')

使用 interp1d 函数，我们创建了两个函数 f1 和 f2。这些函数，对于给定的输入 x 返回 y。第三个变量 kind 表示插值技术的类型。'Linear', 'Nearest', 'Zero', 'Slinear', 'Quadratic', 'Cubic' 是一些插值过程中使用到的技术。

现在，让我们创建一个新的更长的输入，看看插值的明显区别。我们将对新数据使用与旧数据相同的功能。

xnew = np.linspace(0, 4,30)

plt.figure("迹忆客-jiyik.com")

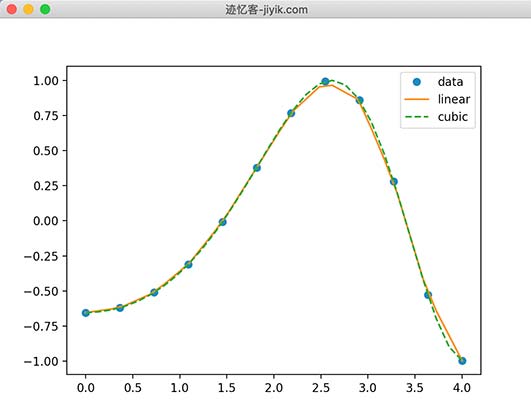
plt.plot(x, y, 'o', xnew, f1(xnew), '-', xnew, f2(xnew), '--')

plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')

plt.show()

执行上面的程序，得到的图形如下所示

样条曲线

为了通过数据点绘制平滑的曲线，绘图员曾经使用称为机械样条的薄而灵活的木条、硬橡胶、金属或塑料条。为了使用机械样条，将销放置在设计中沿曲线选择的点上，然后将样条弯曲，使其接触到这些销中的每一个销。

显然，通过这种结构，样条在这些引脚处插入曲线。它可用于在其他图纸中再现曲线。销钉所在的点称为结点。我们可以通过调整节点的位置来改变由样条定义的曲线的形状。

单变量样条

一维平滑样条拟合一组给定的数据点。scipy.interpolate 中的 UnivariateSpline 方法是一种基于固定数据点类创建函数的便捷方法 ，其语法如下

scipy.interpolate.UnivariateSpline(x, y, w = None, bbox = [None, None], k = 3, s = None，ext = 0，check_finite = False)

UnivariateSpline() 方法参数如下

• 这将 k 次的样条 y = spl(x) 拟合到提供的 x, y 数据。
• w - 指定样条拟合的权重。必须是正的。如果没有（默认），权重都是相等的。
• s - 通过指定平滑条件来指定结的数量。
• k - 平滑样条的度数。必须 <= 5。默认值为 k = 3，三次样条。
• Ext - 控制不在结序列定义的区间内的元素的外推模式。
  • 如果 ext = 0 或 'extrapolate'，则返回外推值。
  • 如果 ext = 1 或“zero”，则返回 0
  • 如果 ext = 2 或 'raise'，则引发 ValueError
  • 如果 ext = 3 of 'const'，则返回边界值。
• check_finite – 检查输入数组是否只包含有限数字。

让我们看下面的例子

import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.figure("迹忆客-jiyik.com")
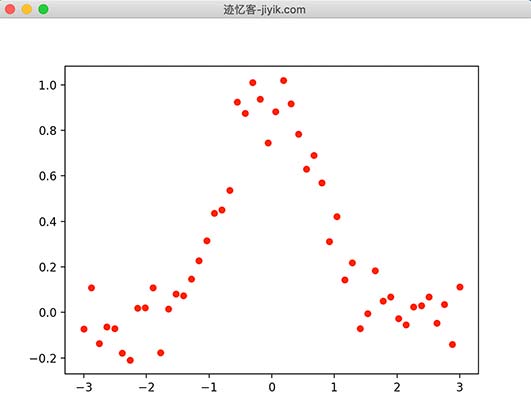
plt.plot(x, y, 'ro', ms = 5)
plt.show()

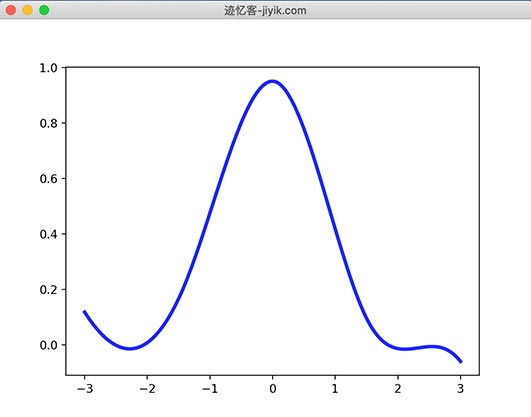
使用平滑参数的默认值。运行结果图如下

spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.figure("迹忆客-jiyik.com")
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()

更改平滑量。运行结果图如下

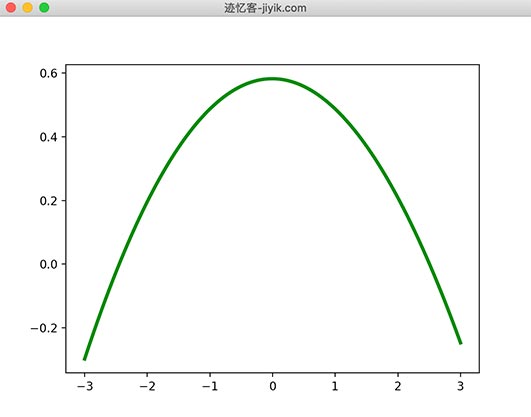
spl.set_smoothing_factor(0.5)
plt.figure("迹忆客-jiyik.com")
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()

运行结果图如下

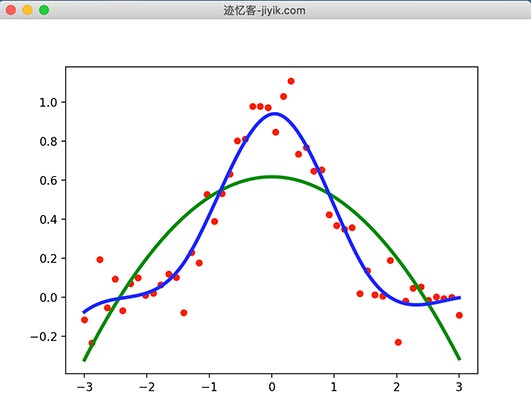
最后我们通过以下程序将三张图合并对比

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

from scipy.interpolate import UnivariateSpline

plt.figure("迹忆客-jiyik.com")

x = np.linspace(-3, 3, 50)
y = np.exp(-x ** 2) + 0.1 * np.random.randn(50)

plt.plot(x, y, 'ro', ms=5)
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw=3)
spl.set_smoothing_factor(0.5)

plt.plot(xs, spl(xs), 'b', lw=3)
plt.show()

结果如下