迹忆客 专注技术分享

当前位置：主页 > 学无止境 > 编程语言 > C++ >
Python PHP Java Go TypeScript C++ Vba Node.js C语言 MATLAB

使用 C++ 将文件读入二叉搜索树

作者：迹忆客 最近更新：2023/08/26 浏览次数：

本文将讨论将文件读入 C++ 中的二叉搜索树。 首先，我们将快速讨论二叉搜索树及其操作。

稍后我们将看到如何将文件读入二叉搜索树。

C++ 中的二叉搜索树

二叉搜索树是一种节点有特殊排列的二叉树，有助于以后的搜索。 这里值得一提的是，统计显示，90%以上的操作都是搜索操作，而； 不到10%的操作包括插入、更新、删除等。

在二叉搜索树中，每个节点的放置方式使得该节点始终大于其左子节点，并且小于等于其右子节点（在重复的情况下）。

该定义递归地应用于树的每个节点。 因此，我们的根总是大于其左子树中的所有节点，并且小于等于其右子树中的所有节点。

     5
   /   \
  3     8
 / \   / \
1   2 6   9

在这里，您可以看到二叉搜索树的示例，这是不言自明的； 如前所述，二叉搜索树有助于搜索操作。

例如，如果我们想在上面的树中搜索 7（说它是键）。 我们将把密钥与根节点 5 进行比较。

键大于根元素； 因此，我们只需要在右子树中搜索键，因为左子树上的所有值都小于根节点。

接下来，我们将密钥与 8 进行比较，并向 8 的左子树移动，因为密钥小于 8。接下来，我们将 6 与密钥进行比较，并向 6 的右子树移动。

在6的右边，我们有NULL； 因此，我们将停止未找到的元素。 我们进行了 3 次比较，而不是 6 次。

树中的元素越多，与树中总元素的比较比例将进一步减少。 搜索看起来微不足道； 不过，我们稍后会给您完整的代码。

在展示完整的代码之前，我们先讨论一下 BST 中的插入和删除操作。 不过，最好先看看 Node 类的定义。

template <class T>
class Node{
public:
    T data;
    Node* left;
    Node* right;
    Node(T data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};

在这里，我们使用了一个模板来对任何数据类型使用相同的树。 当我们使用 BST 时，我们将向您展示它的好处。

在 Node 类的定义中，我们有模板类型的数据，我们可以在创建对象时选择这些数据。 我们有左指针和右指针，因为我们将实现树链接的实现。

在构造函数中，除了 data 之外，我们还给 left 和 right 指针赋值 NULL，因为 start 中的每个新节点都没有左右子节点。

C++ 中二叉搜索树的插入

考虑在 BST 中插入新元素。 有两种可能的情况：树为空或有一个或多个节点。

第一种情况是树为空； 插入后新元素将成为树的根节点。 在第二种情况下，新节点将成为某个现有节点的左子节点或右子节点。

因此，我们将从根节点开始，将该节点的值与我们的新值进行比较； 我们将移动到当前节点的左侧或当前节点的右侧。

最后，我们将到达一个点，我们有 NULL（没有节点）； 我们将创建一个新节点，并根据该节点和新节点的值将其设为左子节点或右子节点。

例如，如果我们在 BST 中插入节点 7，则新的 BST 将是：

     5
   /   \
  2     8
 / \   / \
1   3 6   9
       \
           7

从根节点开始，5小于7，所以向右移动。 8 更大，所以我们移到左侧。 6较小； 因此，向右移动。

右侧没有节点，因此我们创建一个新节点，并将其作为节点 6 的右子节点。我们将看到插入函数的实现，但在此之前，请参阅类 BST 的定义。

template <class T>
class BST{
    Node<T> *root;
public:
    BST(){    root = NULL;    }
    ...

我们再次为 BST 创建了一个模板类，其中只有 Node<T> 类型的数据成员根。 在构造函数中，我们将 NULL 分配给根节点，这意味着树是空的。

因此，在删除的情况下，每当我们删除最后一个节点时，我们都会将 NULL 分配给根节点。 我们来看看插入函数。

Node<T>* insert(T key){            root = insert(root, key);    }

Node<T>* insert(Node<T>* temp, T key){
    if (temp == NULL)        return new Node<T>(key);
    if (temp->data> key)    temp->left = insert(temp->left, key);
    else                     temp->right = insert(temp->right, key);
    return temp;
}

首先，我们有一个包装函数来调用主力函数，该函数执行插入任务。 编写包装函数的原因是，出于安全原因，我们不想授予类外部对根节点的访问权限。

在我们的主力函数中，我们有一个递归实现，其中基本情况是 NULL 节点，我们将在其中创建一个新节点并将其地址返回给调用者，调用者会将此地址分配给左子节点或右子节点以链接新节点 树中的节点。

如果我们没有 NULL 节点，我们将比较数据并根据当前节点的值是较小还是较大而向右或向左移动，正如我们已经讨论过的搜索策略。

C++ 中二叉搜索树的删除

与插入一样，删除 BST 中的元素也有两种可能的情况。 我们要么删除最后一个节点，即根节点，要么删除树中具有多个节点的某个节点，这样删除当前节点后树就不会变空。

在第一种情况下，我们删除该节点并将 NULL 分配给根节点。 对于第二种情况，我们有三种可能：

  1. 节点没有子节点
  2. 节点只有一个子节点
  3. 节点同时具有左子节点和右子节点

前两个方案非常简单。 如果没有子节点。

删除节点并返回NULL（因为我们再次递归定义），以便在调用函数时，父节点将NULL分配给它的右或左指针。

如果该节点有一个子节点，则将子节点替换为当前节点，并删除当前节点。 结果，子节点将被分配给祖父而不是父亲，因为父亲会死（抱歉这个类比）。

最后一种情况很棘手，即一个节点同时具有左子节点和右子节点。 在这种情况下，我们有两个选择。

首先，从当前节点的右子树中选择最左边的后代节点或从左子树中选择最右边的后代节点。 在这两种情况下，都将选择节点的值复制到当前节点。

现在，BST 中有两个具有相同值的节点； 因此，我们将在当前节点的左子树或右子树处再次调用递归删除函数。

考虑这个例子； 假设我们要从根节点删除 5。 我们可以从右子树中选择节点 6，即 5 的右子树中最左边的节点，或者我们可以从左子树中选择节点 3，即左子树中最右边的节点 5 的树。

     5                 3                 6
   /   \              /  \             /  \
  2     8          2     8          2     8
 / \   / \         /     / \         / \     \
1   3 6   9        1     6   9        1   3     9

我们来看看删除函数的实现。

Node<T>* deleteNode(T key){    root = deleteNode(root, key);    }
Node<T>* deleteNode(Node<T>* temp, T key){
    if (temp == NULL)                        return temp;
    if (temp->data>key)            temp->left = deleteNode(temp->left, key);
    else if (temp->data<key)        temp->right = deleteNode(temp->right, key);
    else{
        if (temp->left == NULL && temp->right == NULL) {
            delete temp;
            temp = NULL;
        }
        else if (temp->left == NULL){
            Node<T>* curr = temp;
            temp = temp->right;
            delete curr;
        }
        else if (temp->right == NULL){
            Node<T>* curr = temp;
            temp = temp->left;
            delete curr;
        }
        else{
            Node<T>* toBeDeleted = findMinNode(temp->right);
            temp->data = toBeDeleted->data;
            temp->right = deleteNode(temp->right, toBeDeleted->data);
        }
    }
    return temp;
}

同样，首先，我们有一个包装函数。 接下来，我们有主力功能。

在前三行中，我们正在搜索目标节点。 在这种情况下，目标值不存在于树中； 最终，我们将到达 NULL 节点。

否则，有三种情况，要么当前节点比key大，要么比key小，要么当前节点是我们的目标节点（这种情况下，我们会移动到另一部分）。

另一方面，我们处理三个案例； 我们已经讨论过目标节点没有子节点，只有右子节点，只有左子节点，并且左右子节点都有（在另一部分处理）。

在这一部分中，我们使用函数 findMinNode 从当前/目标节点的右子树中选择最小的节点。 现在，看看 BST 的全班。

#include<iostream>
using namespace std;

template <class T>
class Node{
public:
    T data;
    Node* left;
    Node* right;
    Node(T data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};
template <class T>
class BST{
    Node<T> *root;
public:
    BST(){    root = NULL;    }
    Node<T>* insert(T key){            root = insert(root, key);    }
    Node<T>* insert(Node<T>* temp, T key){
        if (temp == NULL)        return new Node<T>(key);
        if (temp->data> key)    temp->left = insert(temp->left, key);
        else                                 temp->right = insert(temp->right, key);
        return temp;
    }
    Node<T>* findMinNode(Node<T>* temp){
        while (temp->left != NULL)    temp = temp -> left;
        return temp;
    }
    Node<T>* deleteNode(T key){    root = deleteNode(root, key);    }
    Node<T>* deleteNode(Node<T>* temp, T key){
        if (temp == NULL)                        return temp;
        if (temp->data>key)            temp->left = deleteNode(temp->left, key);
        else if (temp->data<key)        temp->right = deleteNode(temp->right, key);
        else{
            if (temp->left == NULL && temp->right == NULL) {
                delete temp;
                temp = NULL;
            }
            else if (temp->left == NULL){
                Node<T>* curr = temp;
                temp = temp->right;
                delete curr;
            }
            else if (temp->right == NULL){
                Node<T>* curr = temp;
                temp = temp->left;
                delete curr;
            }
            else{
                Node<T>* toBeDeleted = findMinNode(temp->right);
                temp->data = toBeDeleted->data;
                temp->right = deleteNode(temp->right, toBeDeleted->data);
            }
        }
        return temp;
    }
    void preOrder(){    preOrder(root);        cout << '\n';}
    void preOrder(Node<T>* temp){
        if (temp == NULL)   return;
        cout << temp->data << " ";
        preOrder(temp->left);
        preOrder(temp->right);
    }
    void inOrder(){    inOrder(root);        cout << '\n';}
    void inOrder(Node<T>* temp){
        if (temp == NULL)   return;
        inOrder(temp->left);
        cout << temp->data << " ";
        inOrder(temp->right);
    }
};
int main(){
     BST<int> tree;
    tree.insert(40);
    tree.insert(22);
    tree.insert(15);
    tree.insert(67);
    tree.insert(34);
    tree.insert(90);
    tree.preOrder();
    tree.inOrder();
    tree.deleteNode(40);
    cout << "After deleting 40 temp from the tree\n";
    tree.preOrder();
    tree.inOrder();
    return 0;
}

我们拥有带有 inOrder 和 preOrder 遍历函数的整个 BST 类来查看树的形状。 我们可以通过中序和前序遍历或者中序和后序遍历来构建 BST； 你可以阅读这篇文章。

让我们看看代码的输出。

40 22 15 34 67 90
15 22 34 40 67 90
After deleting 40 temp from the tree
67 22 15 34 90
15 22 34 67 90

在此输出中，第一行具有前序遍历，第二行具有中序遍历。 首先，有序 BST 总是给出排序的元素。

因此，第二行以某种方式确认我们的代码正在正确执行插入。

我们可以从前两行（遍历）构建二叉树。 前序总是从根节点开始遍历； 因此，40是根节点。

如果我们在中序遍历中看到 40（第二行），我们可以将二叉树分为左子树和右子树，其中 67 和 90 位于右子树，15、22 和 34 位于左子树 -子树； 同样，我们可以完成剩下的二叉树。 最后，我们的二叉树是：

     40
   /   \
  22    67
 / \      \
15  34    90

这棵二叉树具有 BST 的性质，表明我们的代码运行良好； 同样，删除40后我们可以构造一棵二叉树。

     67
   /   \
  22    90
 / \
15  34

节点 40 是我们的目标节点，具有左右子节点。 我们从右子树中选择了最左边的，即67，因为67没有左子树； 因此，我们将值 67 复制到目标节点，并再次调用删除函数以从根的右子树中删除 67。

现在，我们有一个例子，67 有唯一的右孩子，90； 因此，我们将 90 替换为 67。结果，90 将成为 67 的右孩子。

用 C++ 将文件读入二叉搜索树

最后，现在我们可以讨论将文件读入 BST 中了。 再说一次，我们会一步一步地去做。

首先，考虑以下文件。

This is first line.
This is second line.
This is third line.
This is fourth line.
This is fifth line.
This is sixth line.
This is seventh line.
This is eighth line.

我们可以使用 getline 函数在 C++ 中轻松读取该文件。 看代码：

#include<iostream>
#include<fstream>
using namespace std;
int main(){
    ifstream in ("sample.txt");
    string s;
    while (getline(in, s))
        cout << s << '\n';
      in.close();
}

我们将得到与您在上一个框中的文件内容中看到的相同的输出。 然而，我们的目标是将文本放入 BST 中，以便我们可以进行更快的搜索。

所以，很简单； 我们已经在类模板中实现了 BST，我们也可以将其用于字符串； 我们所要做的就是相应地创建一个 BST 对象。

您可以将内容保存在 sample.txt 文件中，以便通过代码读取该文件。 在这里，我们有将文件读入二叉搜索树的代码。

#include<iostream>
#include<fstream>
using namespace std;

template <class T>
class Node{
public:
    T data;
    Node* left;
    Node* right;
    Node(T data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};
template <class T>
class BST{
    Node<T> *root;
public:
    BST(){    root = NULL;    }
    Node<T>* insert(T key){            root = insert(root, key);    }
    Node<T>* insert(Node<T>* temp, T key){
        if (temp == NULL)        return new Node<T>(key);
        if (temp->data> key)    temp->left = insert(temp->left, key);
        else                                 temp->right = insert(temp->right, key);
        return temp;
    }
    Node<T>* findMinNode(Node<T>* temp){
        while (temp->left != NULL)    temp = temp -> left;
        return temp;
    }
    Node<T>* deleteNode(T key){    root = deleteNode(root, key);    }
    Node<T>* deleteNode(Node<T>* temp, T key){
        if (temp == NULL)                        return temp;
        if (temp->data>key)            temp->left = deleteNode(temp->left, key);
        else if (temp->data<key)        temp->right = deleteNode(temp->right, key);
        else{
            if (temp->left == NULL && temp->right == NULL) {
                delete temp;
                temp = NULL;
            }
            else if (temp->left == NULL){
                Node<T>* curr = temp;
                temp = temp->right;
                delete curr;
            }
            else if (temp->right == NULL){
                Node<T>* curr = temp;
                temp = temp->left;
                delete curr;
            }
            else{
                Node<T>* toBeDeleted = findMinNode(temp->right);
                temp->data = toBeDeleted->data;
                temp->right = deleteNode(temp->right, toBeDeleted->data);
            }
        }
        return temp;
    }
    void preOrder(){    preOrder(root);        cout << '\n';}
    void preOrder(Node<T>* temp){
        if (temp == NULL)   return;
        cout << temp->data << " ";
        preOrder(temp->left);
        preOrder(temp->right);
    }
    void inOrder(){    inOrder(root);        cout << '\n';}
    void inOrder(Node<T>* temp){
        if (temp == NULL)   return;
        inOrder(temp->left);
        cout << temp->data << " ";
        inOrder(temp->right);
    }
};
int main(){
    BST<string> tree;
    ifstream in ("sample.txt");
    string s;
    while (getline(in, s))
        tree.insert(s);
    tree.preOrder();
    tree.inOrder();
     in.close();
    return 0;
}

输出:

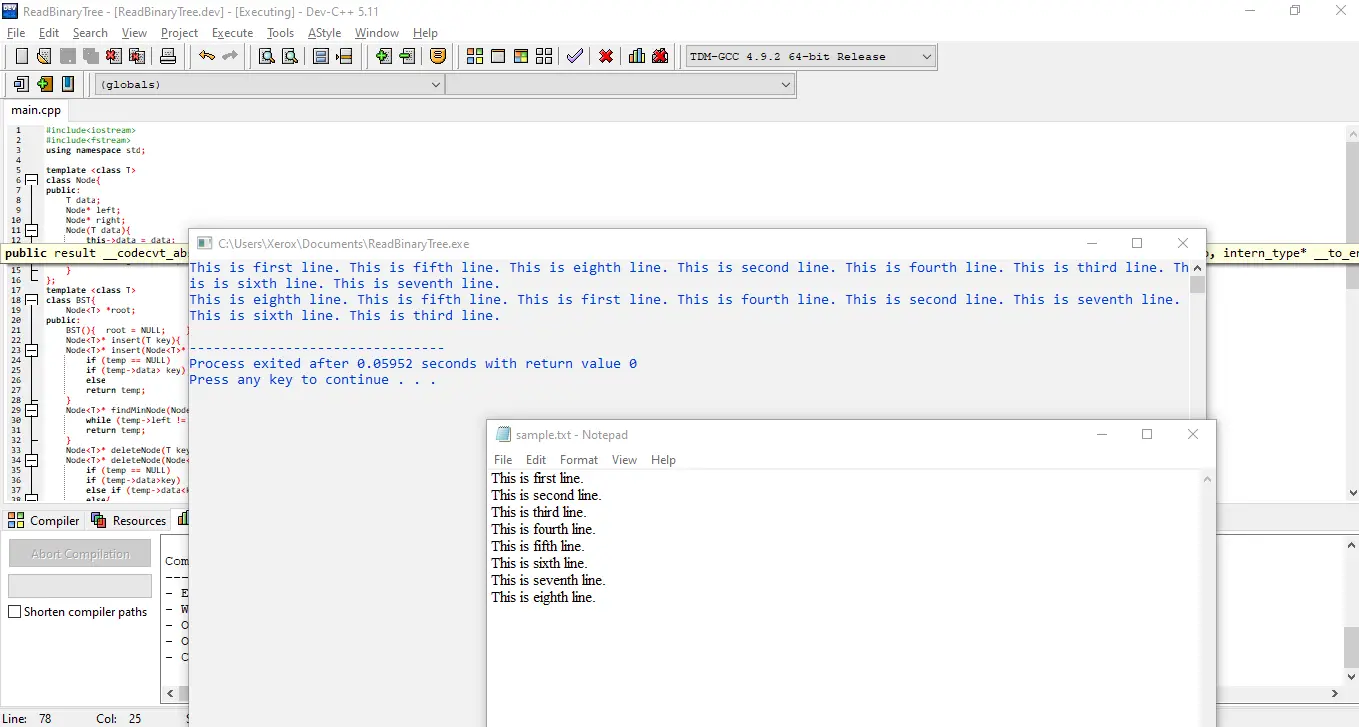
将文件读入二叉搜索树

同样，首先，我们进行前序遍历，这表明根节点是这是第一行； 但是，如果我们看到有序遍历，我们就会按排序顺序输出。

也就是说，从 e 开始的第八个，是第一个、第二个、第三个、第四个、第五个、第六个、第七个和第八个中最小的字母，而接下来，我们有第五个，它比第一个小，因为第五个中的 f 比第五个中的 r 小 第一的。

上一篇：C++中逐级打印二叉树中的数据

下一篇：C++ 中的向量迭代器

转载请发邮件至 1244347461@qq.com 进行申请，经作者同意之后，转载请以链接形式注明出处

本文地址：

相关文章

C++ 二叉搜索树析构函数

发布时间：2023/08/31 浏览次数：176 分类：C++

本文将讨论使用 C++ 中的 delete 关键字为二叉搜索树创建析构函数。C++ 二叉搜索树析构函数

确定 Java 中二叉搜索树的高度

发布时间：2023/08/11 浏览次数：64 分类：Java

在这篇深入的文章中，我们将在实现递归搜索程序以确定 Java 程序中树的高度之前学习二叉搜索树的基础知识。 要理解本文，我们建议大家对树的数据结构概念有基本的了解。二叉搜索树

将二叉树转换为二叉搜索树

发布时间：2023/03/20 浏览次数：185 分类：算法

本教程教大家如何将二叉树转换为二叉搜索树。二叉树是一种非线性数据结构。它被称为二叉树，因为每个节点最多有两个子节点。这些子节点被称为左子和右子。

二叉搜索树删除

发布时间：2023/03/20 浏览次数：189 分类：算法

本教程介绍了二叉搜索树的删除操作。

二叉搜索树检查

发布时间：2023/03/20 浏览次数：161 分类：算法

如何检查给定的二叉树是否是二叉搜索树。

二叉搜索树

发布时间：2023/03/20 浏览次数：121 分类：算法

本教程介绍了数据结构 Binary Search Tree。

扫一扫阅读全部技术教程

社交账号
  • https://www.github.com/onmpw
  • qq:1244347461

最新推荐

教程更新

热门标签

Js Javascript Prototype Vue WEB Python Pandas Mysql Jquery Angular Flask Django CSharp C# Batch Linux Bash C++ arduino Numpy powershell R Rust Ruby
扫码一下
查看教程更方便