迹忆客 专注技术分享

本篇文章将介绍拓扑排序算法在 Python 中的实现。

Python 中的拓扑排序算法

拓扑排序算法对有向无环图 (DAG) 进行排序。 有向无环图 (DAG) 是一种具有从一个节点到另一个节点的有向边但没有环的图。

拓扑排序是一种接受 DAG 作为输入并返回数组的算法，其中每个节点都出现在它指向的节点之前。

它不能应用于 DAG 以外的任何图，因为在拓扑排序中，排序完全取决于节点之间边的方向，并且如果图内有循环，则可以有多种排列。

因此，我们可以说有向无环图节点的拓扑排序是按顺序排列节点的操作，如果边 (i,j) 存在，则 i 在列表中排在 j 之前。

拓扑排序本质上提供了执行任务的顺序，并帮助我们确定图是否有环。

每个图可能支持不止一种拓扑排序。 图中节点的入度决定了它。

此外，网络的拓扑排序从入度为 0 的节点开始，即没有传入边的节点。

让我们看一个例子，以更好地理解拓扑排序中发生的事情。

Input DAG:

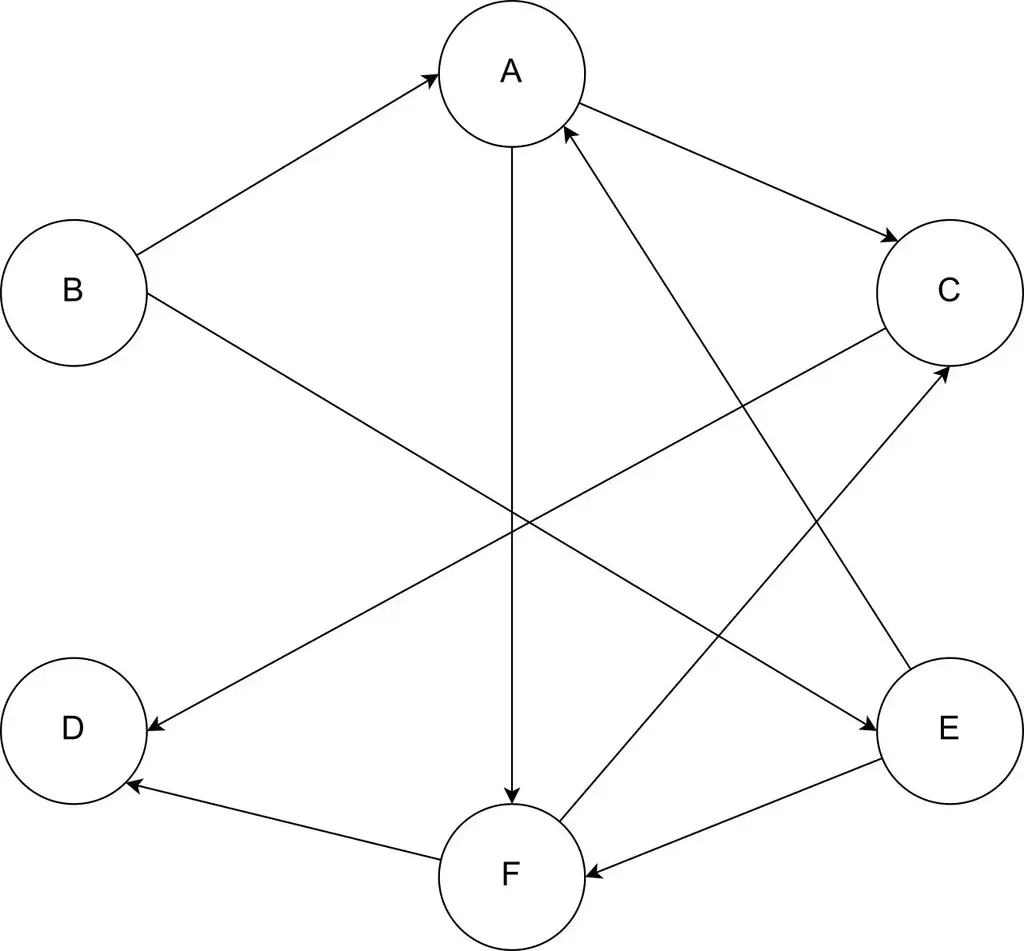
First Iteration: []

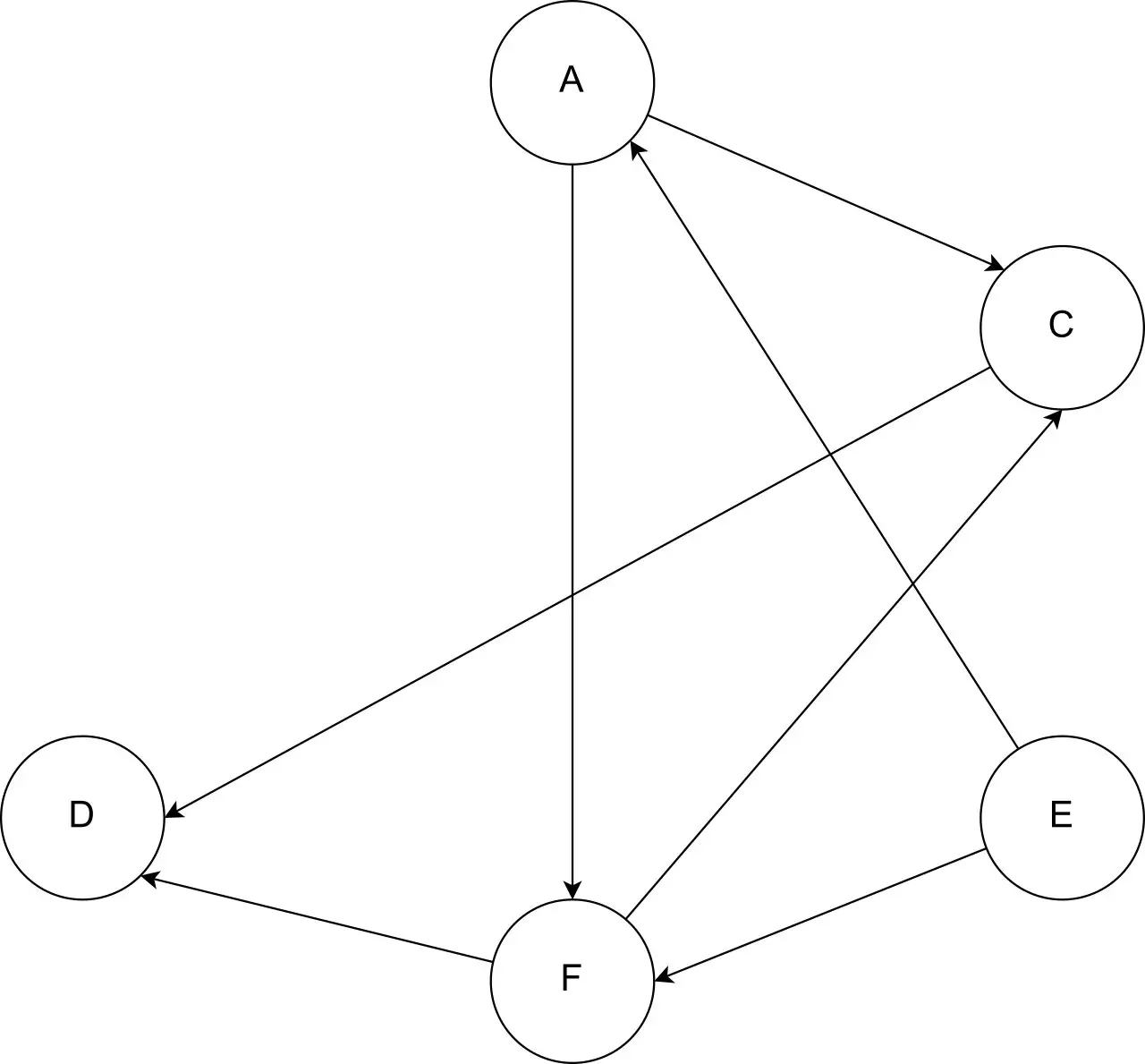
Second Iteration: [B]

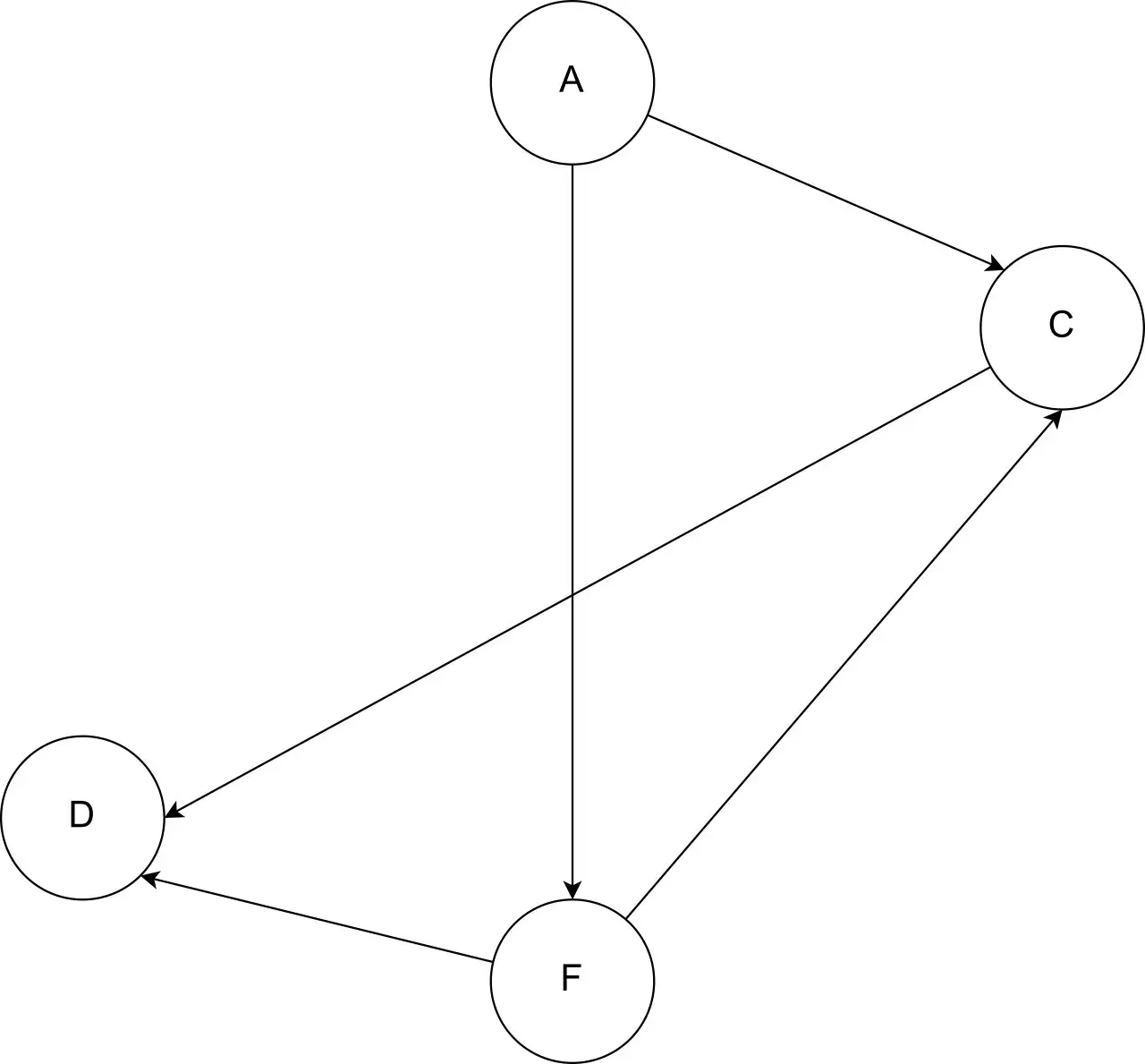
Third Iteration: [B, E]

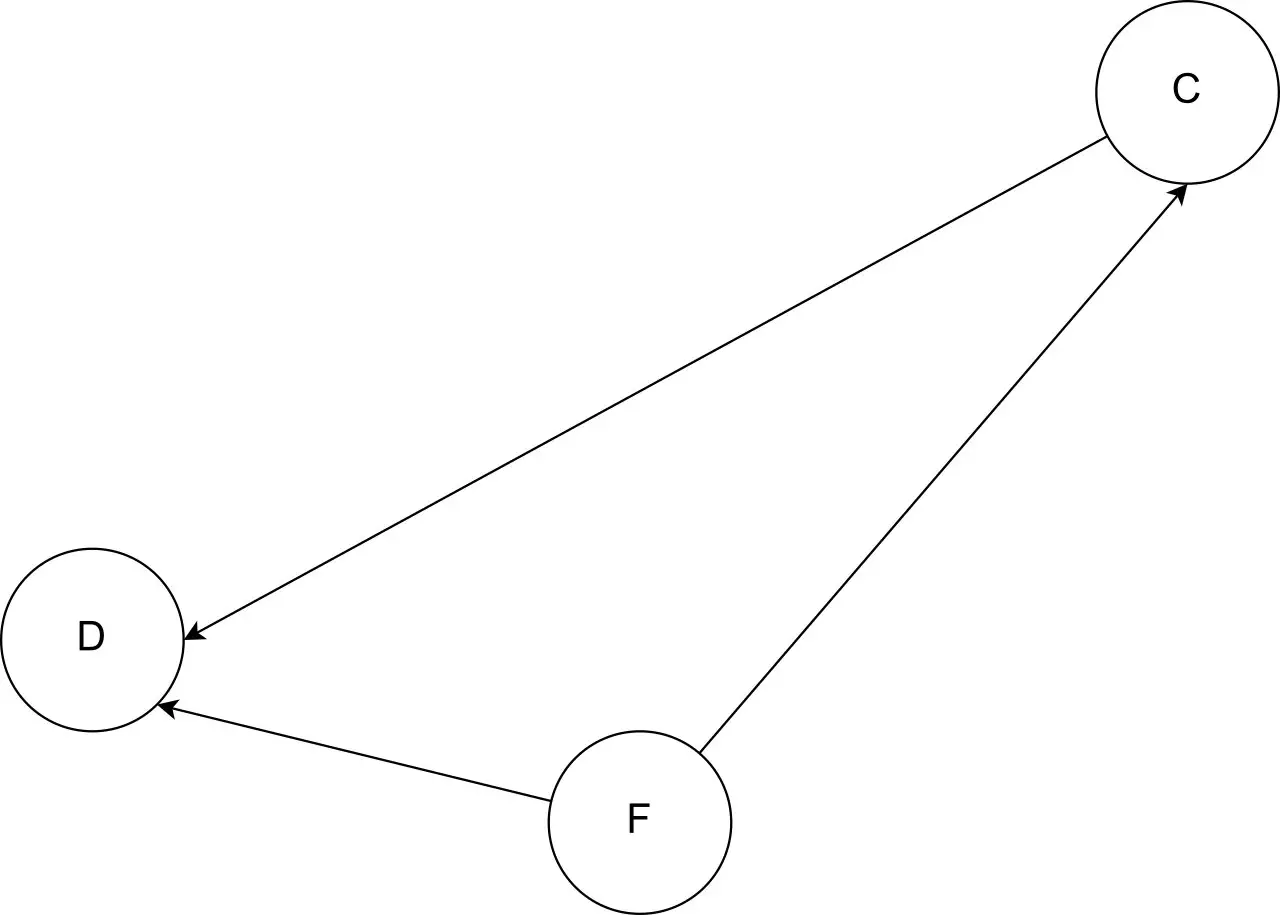
Fourth Iteration: [B, E, A]

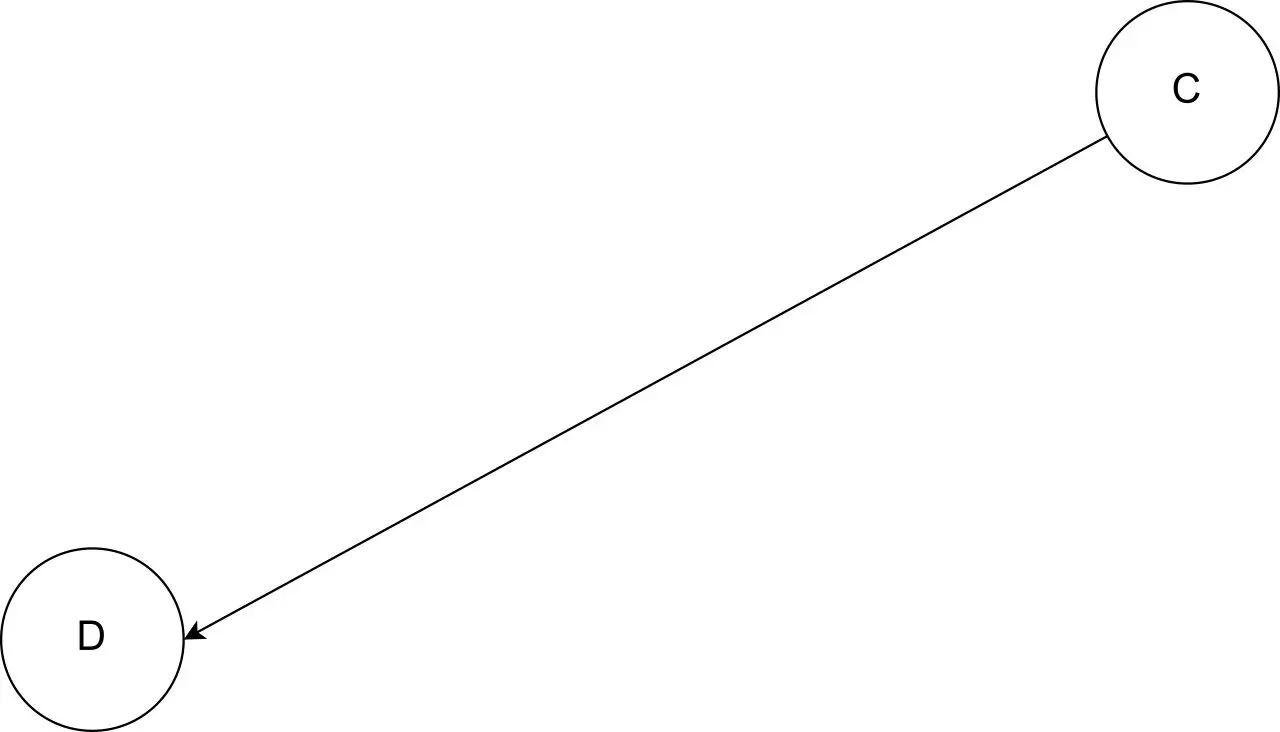
Fifth Iteration: [B, E, A, F]

Final Output: [B, E, A, F, C, D]

在上面的例子中，我们迭代地从我们的图中删除没有输入边的节点并将其放入我们的数组中。 我们重复这一过程，直到图中只剩下一个节点。

最后，我们将这个最终节点附加到数组的末尾。

在 Python 中实现拓扑排序算法

我们可以实现上面讨论的相同逻辑，以在 Python 中创建拓扑排序程序。 下面给出了在我们的代码中实现该算法的步骤。

1. 识别没有传入边的节点。
2. 从图中删除此节点及其对应的边。
3. 更新相邻节点的入度。
4. 重复步骤 1 到 3，直到图形为空。

从这 4 个步骤可以清楚地看出，我们必须为拓扑排序创建一个图。 这可以通过多种方式完成，但最方便的方法是创建一个图类，其中包含用于将节点和边插入到我们的图中的方法。

以下代码片段显示了一个带有构造函数和向我们的图形添加更多边的方法的图形类。

from collections import defaultdict

class Graph:

    def __init__(self, directed=False):
        self.graph = defaultdict(list)
        self.directed = directed

    def addEdge(self, frm, to):
        self.graph[frm].append(to)
        if self.directed is False:
            self.graph[to].append(frm)
        else:
            self.graph[to] = self.graph[to]

现在，我们有一个名为 graph 的类可以初始化有向或无向图，还有一个方法 addEdge() 可以用来向我们的图添加更多的边。

我们现在需要的只是一种实现拓扑排序算法的机制。 我们需要创建一个访问节点的函数，检查是否没有传入边，如果没有任何传入边，则删除该节点。

此类函数显示在以下代码片段中。

def visitNode(self, s, visited, sortlist):
    visited[s] = True
    for i in self.graph[s]:
        if not visited[i]:
            self.visitNode(i, visited, sortlist)
    sortlist.insert(0, s)

上面的函数取当前节点s的索引； 一个布尔列表 visited 包含有关节点是否已被访问的信息，以及我们将用于存储从图中删除的节点的排序列表。

我们需要创建另一个辅助函数，它会为图中的所有节点增量调用此 visitNode() 并在最后打印排序列表的值。 以下代码片段显示了用 Python 实现的类似功能。

def topologicalSort(self):
    visited = {i: False for i in self.graph}
    sortlist = []

    for v in self.graph:
        if not visited[v]:
            self.visitNode(v, visited, sortlist)
    print(sortlist)

现在，我们对图形类的实现已经完成。 我们现在需要创建一个图形并调用 topologicalSort() 函数来对我们的列表进行排序。

此过程已在以下代码中实现。

if __name__ == '__main__':

    graph = Graph(directed=True)
    graph.addEdge(1, 6)
    graph.addEdge(1, 3)
    graph.addEdge(2, 1)
    graph.addEdge(2, 5)
    graph.addEdge(3, 4)
    graph.addEdge(5, 1)
    graph.addEdge(5, 6)
    graph.addEdge(5, 6)
    graph.addEdge(6, 3)
    graph.addEdge(6, 4)

    print("Topological Sort Algorithm:")
    graph.topologicalSort()

输出:

Topological Sort Algorithm:
[2, 5, 1, 6, 3, 4] #[B, E, A, F, C, D] in terms of previous example

我们在此代码中创建的图表对应于上面给出的图表中的图表。 这里，索引 1 到 6 指的是节点 A 到 F。

正如我们所见，最终排序的列表是 [B, E, A, F, C, D]，这与我们在代码中的输出相同。

现在，让我们看看上面的代码组合在一个代码块中。

from collections import defaultdict
class Graph:

    def __init__(self, directed=False):
        self.graph = defaultdict(list)
        self.directed = directed

    def addEdge(self, frm, to):
        self.graph[frm].append(to)
        if self.directed is False:
            self.graph[to].append(frm)
        else:
            self.graph[to] = self.graph[to]

    def visitNode(self, s, visited, sortlist):
        visited[s] = True
        for i in self.graph[s]:
            if not visited[i]:
                self.visitNode(i, visited, sortlist)
        sortlist.insert(0, s)

    def topologicalSort(self):
        visited = {i: False for i in self.graph}
        sortlist = []

        for v in self.graph:
            if not visited[v]:
                self.visitNode(v, visited, sortlist)
        print(sortlist)

if __name__ == '__main__':

    graph = Graph(directed=True)
    graph.addEdge(1, 6)
    graph.addEdge(1, 3)
    graph.addEdge(2, 1)
    graph.addEdge(2, 5)
    graph.addEdge(3, 4)
    graph.addEdge(5, 1)
    graph.addEdge(5, 6)
    graph.addEdge(5, 6)
    graph.addEdge(6, 3)
    graph.addEdge(6, 4)

    print("Topological Sort Algorithm:")
    graph.topologicalSort()

输出:

Topological Sort Algorithm:
[2, 5, 1, 6, 3, 4] #[B, E, A, F, C, D] in terms of previous example

我们的教程到此结束。 现在，您可以在完全了解其工作原理的情况下实现拓扑排序。