在 Python 中实现多项式回归
本文将重点介绍多项式回归以及我们如何使用 Python 将其应用于真实世界的数据。
首先，我们将了解回归是什么以及它与多项式回归有何不同。 然后，我们将看到我们特别需要多项式回归的情况。
我们将看到多个编程示例，以更好地理解这个概念。
回归的定义
回归是一种统计方法，用于确定自变量或特征与因变量或结果之间的关系。 在机器学习中，它被用作预测建模的方法，其中使用算法来预测连续结果。
在监督机器学习中，回归问题的解决是机器学习模型中最常见的应用之一。
我们训练算法以找到因变量和自变量之间的关系，以根据一些看不见的输入数据集预测一些结果。
回归模型主要用于预测分析模型，其中应用程序需要根据一些输入数据或历史数据来预测未来数据。 例如，组织可以使用回归分析根据当前销售数据预测下个月的销售额。
医疗公司可以使用回归模型来预测特定时期内公众的健康趋势。 回归技术的典型用途是：
- 预测连续的结果，例如财产价值、股票价格或销售额；
- 预测未来零售销售或营销活动的绩效，以最大限度地利用资源；
- 预测客户或用户模式，例如流媒体服务或购物网站；
- 分析数据集以找出变量和输出之间的关系；
- 根据各种因素预测利率和股票价格；
- 创建时间序列的可视化。
回归类型
回归技术有很多，但主要分为三大类：
- 简单线性回归
- 逻辑回归
- 多元线性回归
简单线性回归
简单线性回归是一种线性回归方法，其中在数据点内绘制直线以最小化直线与数据点之间的误差。 它是机器学习回归的最基本和最直接的形式之一。
在这种情况下，自变量和因变量被认为具有线性关系。
逻辑回归
当因变量只能有两个值，真或假，或者是或否时，使用逻辑回归。 可以使用逻辑回归模型预测因变量发生的机会。
在大多数情况下，输出值必须是二进制的。 可以使用 S 形曲线映射因变量和自变量之间的关系。
多元线性回归
当使用多个自变量时，使用多元线性回归。 多元线性回归技术包括多项式回归。
当自变量很多时，就是多元线性回归。 当存在大量自变量时，它比基本线性回归更适合。
当以二维显示时，结果是一条适合数据点的曲线。
在简单回归中，我们使用以下公式使用自变量查找因变量的值：
$$
y = a+bx+c
$$
在这里
- y 是因变量
- a 是 y 截距
- b 是斜率
- c是错误率
在许多情况下，线性回归不会在存在多个自变量的情况下给出完美的结果，因为需要多项式回归，其公式为：
$$
y = a_0 + a_1x_1 + a_2x_2^2 + …..+ a_nx_n^n
$$
正如我们所见，y 是 x 的因变量。
该多项式的次数应具有最佳值，因为较高的次数会过度拟合数据。 度值越低，模型对结果的拟合就越差。
在 Python 中实现多项式回归
Python 包含用于确定数据点之间的链接和绘制多项式回归线的函数。 我们将向您展示如何使用这些策略，而不是复习数学公式。
在下面的示例中，有 18 辆汽车在通过收费站时被登记。 我们记录了汽车的速度和它经过我们时的时间（小时）。
一天中的小时数在 x 轴上表示，速度在 y 轴上表示：
import matplotlib.pyplot as plot
xAxis = [10,20,30,50,60,70,80,90,100,120,130,140,150,160,180,190,210,220]
yAxis= [96,95,84,65,60,59,65,55,71,75,78,86,88,79,95,98,99,100]
plot.scatter(xAxis, yAxis)
plot.show()
输出:
现在，我们将使用 NumPy 和 Matplotlib 绘制多项式回归。
import numpy
import matplotlib.pyplot as plot
xAxis = [10,20,30,50,60,70,80,90,100,120,130,140,150,160,180,190,210,220]
yAxis= [96,95,84,65,60,59,65,55,71,75,78,86,88,79,95,98,99,100]
model = numpy.poly1d(numpy.polyfit(xAxis, yAxis, 3))
linesp = numpy.linspace(10, 220, 100)
plot.scatter(xAxis, yAxis)
plot.plot(linesp, model(linesp))
plot.show()
输出:
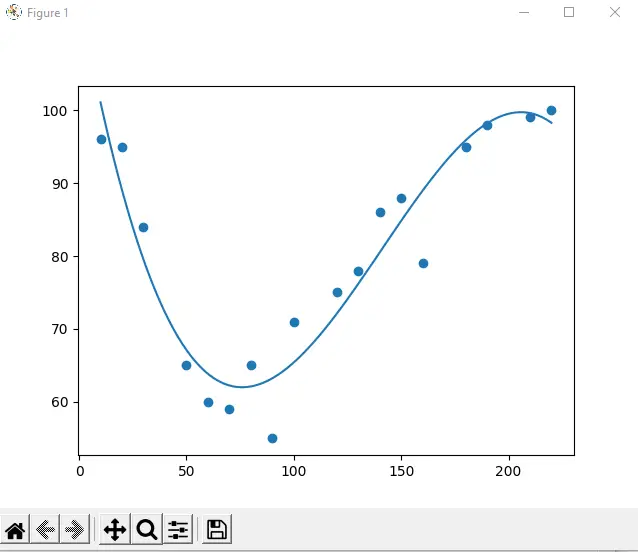
在上面的示例中，我们使用 NumPy 和 Matplotlib 库通过导入语句绘制多项式回归。 之后，我们为 x 轴和 y 轴创建了数组，例如：
xAxis = [10,20,30,50,60,70,80,90,100,120,130,140,150,160,180,190,210,220]
yAxis= [96,95,84,65,60,59,65,55,71,75,78,86,88,79,95,98,99,100]
现在，我们已经使用 NumPy 库的一种方法来制作多项式模型：
model = numpy.poly1d(numpy.polyfit(xAxis, yAxis, 3))
现在我们将指定如何显示该行。 在我们的例子中，我们从 10 开始到 220。
linesp = numpy.linspace(10, 220, 100)
最后三行代码用于绘制绘图，然后是回归线，然后显示绘图。
plot.scatter(xAxis, yAxis)
plot.plot(linesp, model(linesp))
plot.show()
x轴和y轴的关系
了解轴（x 和 y）之间的关系至关重要，因为如果它们之间没有关系，则无法预测未来值或回归结果。
我们将计算一个称为 R-Squared 的值来衡量这种关系。 它的范围从 0 到 1，其中 0 表示没有关系，1 表示 100% 相关。
import numpy
import matplotlib.pyplot as plot
from sklearn.metrics import r2_score
xAxis = [10,20,30,50,60,70,80,90,100,120,130,140,150,160,180,190,210,220]
yAxis= [96,95,84,65,60,59,65,55,71,75,78,86,88,79,95,98,99,100]
model = numpy.poly1d(numpy.polyfit(xAxis, yAxis, 3))
print(r2_score(yAxis, model(xAxis)))
输出:
0.9047652736246418
0.9 的值显示 x 和 y 之间的强关系。
如果值很低，说明关系很弱。 此外，它表明该数据集不适合多项式回归。
相关文章
Django 中的 Slug
发布时间：2023/05/04 浏览次数：173 分类：Python
-
本篇文章旨在定义一个 slug 以及我们如何使用 slug 字段在 Python 中使用 Django 获得独特的帖子。
在 Django 中按降序过滤查询集中的项目
发布时间：2023/05/04 浏览次数：157 分类：Python
-
在这个讲解中，学习如何借助 Django 中的 order_by() 方法按降序过滤出查询集中的项目。
Django ALLOWED_HOSTS 介绍
发布时间：2023/05/04 浏览次数：181 分类：Python
-
本文展示了如何创建您的 Django 网站，为公开发布做好准备，如何设置 ALLOWED_HOSTS 以及如何在使用 Django 进行 Web 部署期间修复预期的主要问题。
Django 中的 Select_related 方法
发布时间：2023/05/04 浏览次数：129 分类：Python
-
本文介绍了什么是查询集，如何处理这些查询以及我们如何利用 select_related() 方法来过滤 Django 中相关模型的查询。
使用 Post 请求将数据发送到 Django 服务器
发布时间：2023/05/04 浏览次数：159 分类：Python
-
在这篇关于Django的讲解中，我们简要介绍了post和get请求以及如何在Django中用post实现CSRF token。
Django 返回 JSON
发布时间：2023/05/04 浏览次数：106 分类：Python
-
在与我们的讨论中，我们简要介绍了 JSON 格式，并讨论了如何借助 Django 中的 JsonResponse 类将数据返回为 JSON 格式。
在 Django 中创建对象
发布时间：2023/05/04 浏览次数：59 分类：Python
-
本文的目的是解释什么是模型以及如何使用 create() 方法创建对象，并了解如何在 Django 中使用 save() 方法。
在 Django 中为多项选择创建字段
发布时间：2023/05/04 浏览次数：75 分类：Python
-
在本文中，我们将着眼于为多项选择创建一个字段，并向您展示如何允许用户在 Django 中进行多项选择。
