迹忆客 专注技术分享

本文将解释魔方问题、它的属性以及它使用 C++ 的实现。 让我们学习魔方问题来实现魔方。

魔方问题

魔方是正整数的二维数组，其中每一行、每一列和对角线的总和都相同。 求和常被称为Magic Sum，指的是每一行、每一列、每一对角线的总和是常数。

魔方的每个位置的整数值必须是唯一的。 如果 N 是魔方的大小，它可以包含从 1 到 N2 的整数。

以下公式计算幻数和。

魔方的大小将指示行数和列数。 如果 N 等于 3，则幻方将具有三行和三列。

现在，让我们用一个例子来解释魔术和。 假设N的值为3，则由上式可计算为：

在这里，15 是神奇的总和。 这意味着每列、每行和对角线之和应等于 15。

大小等于3的魔方如下图所示。

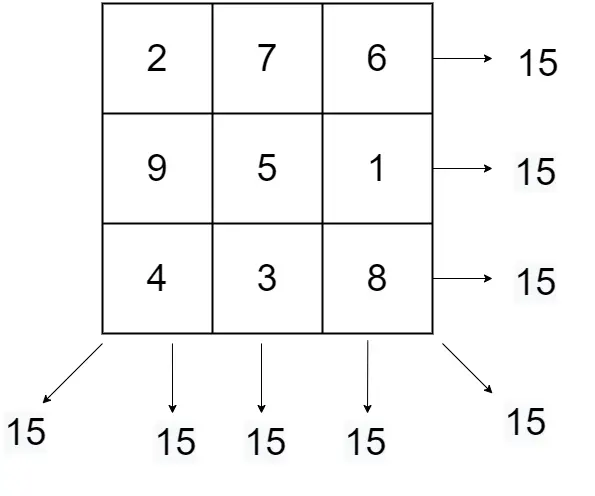
我们可以看到每一行、每一列、每一对角线的和都等于幻数和，而且每一项都是唯一的。

了解了幻方问题之后，现在我们来实现一下。

让我们将要实现的幻方的大小为 n。 然后，第一个值（即 1）存储在幻方中的位置（n/2，n-1）。

假设这个位置是 (i,j)，那么下一个值将在位置 (i-1,j+1)。 这里我们假设每一行和每一列都有一个环绕（即，也称为圆圈时尚）。

魔方问题的条件

1. 下一个值的位置由当前列号加 1 和当前行号减 1 来确定。
   • 如果列的新位置变为 n，那么它将被包装为 0，因为列和行是循环的。
   • 同样，如果乌鸦的新位置变成了-1，它就会被包裹到n-1。
2. 假设新计算的位置已经包含一个值。 在这种情况下，当前行号将通过加 1 来更新，而当前列号将通过从中减去 2 来更新。
3. 如果新计算出来的列号是n，行号是-1，那么更新的位置就是(0,n-2)。

C++中魔方的实现

在进入细节之前，让我们先看看下面的代码：

#include <bits/stdc++.h>
using namespace std;
// This function will generate an old-size magic square only.
void magicSquareGenerator(int s)
{
    int magic_Square[s][s];
    // This will initialize all locations of the magic square to 0
    memset(magic_Square, 0, sizeof(magic_Square));
    // here, r is the row index, and c is the column index for the first number
    int r = s / 2;
    int c = s - 1;
    //  generating magic square
    for (int num = 1; num <= s * s;) {
        if (r == -1 && c == s) // Third condition
        {
            c = s - 2;
            r = 0;
        }
        else {
            if (c == s)
                c = 0;
            if (r < 0)
                r = s - 1;
        }
        if (magic_Square[r][c]) // second condition
        {
            c -= 2;
            r++;
            continue;
        }
        else
            magic_Square[r][c] = num++;
        c++;
        r--; // 1st condition
    }

    // Print magic square
    cout << "The Magic Square has:"<<s<<" rows and "<<s<<" columns.";
    cout <<"\nThe Magic Sum is: "<< s * (s * s + 1) / 2 << ":\n";
    for (r = 0; r < s; r++) {
        for (c = 0; c < s; c++)
            // displaying the magic square.
            cout << setw(4) << magic_Square[r][c] << " ";
        cout << endl;
    }
}

int main()
{ //Code expects only odd sizes
    int s;
    cout<<"Enter the size of the Magic Square: ";
    cin>>s;
    while(s%2==0){
        cout<<"Plz Enter an odd number :"<<endl;
        cout<<"Enter the size of the Magic Square: ";
        cin>>s;
    }
    magicSquareGenerator(s);
    return 0;
}

下面是对上述魔方程序的逐步解释。

1. 值 1 的位置 = (3/2,3-1) = (1,2) = [1][2]。
2. 值 2 的位置 = (1-1,2+1) = (1,2) = [1][2]。
3. 值 3 的位置 = (0-1,0+1) = (3-1,1+1) = [2][1]。
4. 值 4 的位置 = (2-1,1+1) = (1,2) = [1][2]。
   • 由于 [1][2] 已经具有值 1，因此根据条件 2，新位置将为 (1+1,2-2) = [2][0]。
5. 值 5 的位置 = (2-1,0+1) = (1,1) = [1][1]。
6. 值 6 的位置 = (1-1,1+1) = (1,2) = [0][2]。
7. 值 7 的位置 = (0-1,2+1) = (-1,3)
   • 条件 3 成立，因此新位置将为 (0,3-2)=[0][1]。
8. 值 8 的位置是 = (0-1,1+1) = (-1,2) = [2][2] 因为条件 1 行被换行。
9. 值 9 的位置是 = (2-1,2+1) = (1,3) = [1][0] 因为条件 1 列被换行。

这是我们输入魔方 3 的大小时的输出。

Enter the size of the Magic Square: 3
The Magic Square has:3 rows and 3 columns.
The Magic Sum is: 15:
   2    7    6
   9    5    1
   4    3    8

这是我们输入魔方 7 的大小时的输出。

Enter the size of the Magic Square: 7
The Magic Square has:7 rows and 7 columns.
The Magic Sum is: 175:
  20   12    4   45   37   29   28
  11    3   44   36   35   27   19
   2   43   42   34   26   18   10
  49   41   33   25   17    9    1
  40   32   24   16    8    7   48
  31   23   15   14    6   47   39
  22   21   13    5   46   38   30

所提出算法的时间和空间复杂度为 $O(n^2)$。