迹忆客 专注技术分享

Python 中使用图数据结构来表示各种现实生活中的对象，例如网络和地图。 我们可以使用邻接矩阵来表示图。

本文将讨论在 Python 中实现邻接矩阵的不同方法。

创建邻接矩阵

考虑下图。

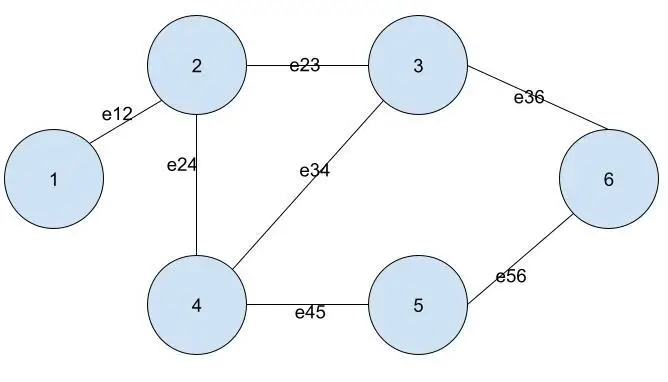
图中，有 6 个节点，编号为 1 到 6。图中连接节点的边有 7 条； 边 eij 连接节点 i 和节点 j。

为了表示该图，我们使用邻接矩阵。

1. 邻接矩阵由二维网格组成。
2. 网格中的每一行或每一列代表一个节点。
3. 对于未加权的图，如上所示，如果网格中位置(i,j)处的值为1，则表示节点i和节点j是连通的。
4. 如果位置(i,j)处的值为0，则节点i和节点j不连接。

如果您想为上图中的图形创建邻接矩阵，它将如下所示。

| 0    | 1    | 0    | 0    | 0    | 0    |
| 1    | 0    | 1    | 1    | 0    | 0    |
| 0    | 1    | 0    | 1    | 0    | 1    |
| 0    | 1    | 1    | 0    | 1    | 0    |
| 0    | 0    | 0    | 1    | 0    | 1    |
| 0    | 0    | 1    | 0    | 1    | 0    |

上表显示位置 (i,j) 处的值也出现在位置 (j,i) 处。 这是由于边eij与边eji相同的原因。

这也会产生沿对角线对称的邻接矩阵。

在未加权图中，边没有权重。 换句话说，所有边都具有相同的权重。

因此，邻接矩阵仅包含值 0 和 1。

现在，考虑以下加权图。

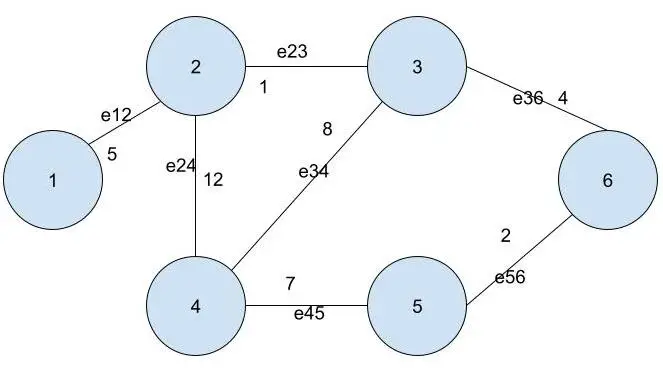
对于加权图，除了边的权重之外，一切都保持不变。 您可以观察到图像中的每个边缘都被分配了一个值。

因此，在邻接矩阵中，位置 (i,j) 处的值就是图中边eij的权重。

上图的邻接矩阵如下所示。

| 0    | 5    | 0    | 0    | 0    | 0    |
| 5    | 0    | 1    | 12   | 0    | 0    |
| 0    | 1    | 0    | 8    | 0    | 4    |
| 0    | 12   | 8    | 0    | 7    | 0    |
| 0    | 0    | 0    | 7    | 0    | 2    |
| 0    | 0    | 4    | 0    | 2    | 0    |

同样，您可以观察到矩阵中位置 (i,j) 处的值也出现在位置 (j,i) 处。 这是由于边eij与边eji相同的原因。

同样，这会产生沿对角线对称的邻接矩阵。

使用 2D 列表在 Python 中创建邻接矩阵

要为具有 n 个节点的未加权图创建邻接矩阵，我们将首先创建一个包含 n 个内部列表的二维列表。 此外，每个内部列表包含 n 个零。

创建包含零的二维列表后，我们将 1 分配给图中存在边 eij 的位置 (i,j)。 对于此任务，我们将使用以下步骤。

• 首先，我们将创建一个名为 adjacency_matrix 的空列表。 之后，我们将使用 for 循环和 append() 方法将其转换为二维列表。
• 在 for 循环内，我们将创建一个名为 row 的空列表。 然后，我们将使用另一个 for 循环用零填充空列表，最后，我们将行追加到 adjacency_matrix 中。
• 在代码中，我们使用元组列表表示边集。 每个元组包含 2 个值，表示图的连接节点。
• 定义边后，我们将使用 for 循环将值 1 分配给图中存在边的位置。

代码：

import pprint
row_num = 6
col_num = 6
adjacency_matrix = []
for i in range(row_num):
    row = []
    for j in range(col_num):
        row.append(0)
    adjacency_matrix.append(row)
edges = [(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
for edge in edges:
    row = edge[0]
    col = edge[1]
    adjacency_matrix[row - 1][col - 1] = 1
    adjacency_matrix[col - 1][row - 1] = 1

print("The edges in the graph are:")
print(edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

输出:

The edges in the graph are:
[(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
The adjacency matrix is:
[[0, 1, 0, 0, 0, 0],
 [1, 0, 1, 1, 0, 0],
 [0, 1, 0, 1, 0, 1],
 [0, 1, 1, 0, 1, 0],
 [0, 0, 0, 1, 0, 1],
 [0, 0, 1, 0, 1, 0]]

在代码中，您可以观察到我们有基于 0 的索引。 因此，每个节点 (i,j) 由邻接矩阵中的位置 (i-1,j-1) 表示。

要为加权图创建邻接矩阵，我们首先创建一个包含 0 的 n x n 二维列表。 之后，我们将分配矩阵中位置 (i,j) 的边 eij 的权重。

您可以在以下示例中观察到这一点。

import pprint

row_num = 6
col_num = 6
adjacency_matrix = []
for i in range(row_num):
    row = []
    for j in range(col_num):
        row.append(0)
    adjacency_matrix.append(row)
weighted_edges = [(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
for edge in weighted_edges:
    row = edge[0]
    col = edge[1]
    weight = edge[2]
    adjacency_matrix[row - 1][col - 1] = weight
    adjacency_matrix[col - 1][row - 1] = weight

print("The edges in the graph are:")
print(weighted_edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

输出:

The edges in the graph are:
[(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
The adjacency matrix is:
[[0, 5, 0, 0, 0, 0],
 [5, 0, 1, 12, 0, 0],
 [0, 1, 0, 8, 0, 4],
 [0, 12, 8, 0, 7, 0],
 [0, 0, 0, 7, 0, 2],
 [0, 0, 4, 0, 2, 0]]

在上面的代码中，边是使用三元组数字表示的。 前 2 个数字表示由边连接的图的节点。

第三个数字代表边的权重。

使用 NumPy 模块在 Python 中创建邻接矩阵

要使用 NumPy 模块为图创建邻接矩阵，我们可以使用 np.zeros() 方法。

np.zeros() 方法采用 (row_num,col_num) 形式的元组作为其输入参数，并返回形状为 row_num x col_num 的二维矩阵。 这里，row_num和col_num是矩阵中的行数和列数。

我们将按照以下步骤使用 np.zeros() 方法创建邻接矩阵。

• 首先，我们将通过将元组 (n,n) 传递给 Zeros() 方法来创建大小为 n x n 的矩阵。
• 然后，我们将图中每条边 eij 在位置 (i-1,j-1) 处的值更新为 1； 在这里，我们使用从 0 开始的索引。 因此，节点 (i,j) 在代码中由位置 (i-1,j-1) 表示。

执行完上述步骤后，我们将得到邻接矩阵，如下例所示。

import pprint
import numpy as np

row_num = 6
col_num = 6
adjacency_matrix = np.zeros((row_num, col_num),dtype=int)
edges = [(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
for edge in edges:
    row = edge[0]
    col = edge[1]
    adjacency_matrix[row - 1][col - 1] = 1
    adjacency_matrix[col - 1][row - 1] = 1

print("The edges in the graph are:")
print(edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

输出:

The edges in the graph are:
[(1, 2), (2, 4), (2, 3), (3, 4), (4, 5), (3, 6), (5, 6)]
The adjacency matrix is:
array([[0, 1, 0, 0, 0, 0],
       [1, 0, 1, 1, 0, 0],
       [0, 1, 0, 1, 0, 1],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 0, 1],
       [0, 0, 1, 0, 1, 0]])

为了创建加权图的邻接矩阵，我们将位置 (i,j) 处的值更新为边 eij 的权重，如下所示。

import pprint
import numpy as np
row_num = 6
col_num = 6
adjacency_matrix = np.zeros((row_num, col_num), dtype=int)
weighted_edges = [(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
for edge in weighted_edges:
    row = edge[0]
    col = edge[1]
    weight = edge[2]
    adjacency_matrix[row - 1][col - 1] = weight
    adjacency_matrix[col - 1][row - 1] = weight

print("The edges in the graph are:")
print(weighted_edges)
print("The adjacency matrix is:")
pprint.pprint(adjacency_matrix)

输出:

The edges in the graph are:
[(1, 2, 5), (2, 4, 12), (2, 3, 1), (3, 4, 8), (4, 5, 7), (3, 6, 4), (5, 6, 2)]
The adjacency matrix is:
array([[ 0,  5,  0,  0,  0,  0],
       [ 5,  0,  1, 12,  0,  0],
       [ 0,  1,  0,  8,  0,  4],
       [ 0, 12,  8,  0,  7,  0],
       [ 0,  0,  0,  7,  0,  2],
       [ 0,  0,  4,  0,  2,  0]])

总结

本文讨论在 Python 中实现邻接矩阵的两种方法。 我们建议您使用 NumPy 模块实现邻接矩阵，因为它在存储要求方面更加高效。

此外，在时间和内存需求方面，在 NumPy 数组上执行不同的操作更加高效。