迹忆客 专注技术分享

本文将讨论二叉树以及我们如何使用它。 我们还将看到如何使用 Python 打印它。

我们将了解在处理二叉树时使用的术语。 我们还将研究使用 Python 代码的二叉树示例。

Python 中的二叉树

Python 的二叉树是可用的最有效的数据结构之一，而且它们的实现也相对简单。 二叉树是一种树状数据结构，具有一个根节点和两个子节点，一个是左节点，一个是右节点。

每个节点可以有任意数量的子节点。 本文将介绍如何在 Python 中创建和遍历二叉树。

让我们更好地理解与树相关的术语。

1. 根：没有父节点的树的最顶层节点。 每棵树都有一个根。
2. 边：边是父子链接。
3. 叶子：没有孩子的节点。 树的最终节点。 树有多个叶节点。
4. 子树：树使用一个节点作为它的根。
5. 深度：深度是节点到根的距离。
6. 高度：节点的高度是到子树最深节点的距离。
7. 树的高度：树的高度是最高节点，对应于根节点的高度。

树的遍历顺序

通过从根节点开始并访问左右子节点来遍历树。 访问节点的顺序称为遍历顺序。

中序遍历树

有几种不同的方法来遍历二叉树。 最常见的是中序遍历，它访问左、根和右子节点。

先序遍历树

另一种标准遍历是先序遍历，先访问根节点，然后是左孩子，最后是右孩子。

中序遍历是访问二叉树中所有节点的最有效方法，因为它只访问每个节点一次。 前序遍历效率稍低，因为它调用了根节点两次。

但是，在遍历过程中我们要修改树时，往往会使用前序遍历，因为很容易先修改根节点，再修改左右子节点。

这是 Python 中顺序遍历的语法和简单实现。

def inorder(node):
  if node is not None:
    inorder(node.left)
    print(node.val)
    inorder(node.right)

所以，当我们想使用中序遍历方法时，我们就是这样编码的。

这是先序遍历：

def preorder(node):
    if node is not None:
        print(node.val)
        preorder(node.left)
        preorder(node.right)

后序遍历

我们还可以按后序遍历树，即访问左孩子、右孩子，然后是根节点。 然而，后序遍历不太常见，因为它的效率低于其他两种遍历。

二叉树的遍历还有其他的方式，比如层序遍历，就是逐层访问树中的节点。 但是，我们不会在本文中介绍这种遍历。

现在我们已经了解了如何遍历二叉树，让我们看看如何创建一棵二叉树并使用 Python 打印它。

二叉树在Python中的实现

我们知道二叉树是什么以及与之相关的术语。 我们将使用 Python 实现二叉树，以更好地理解二叉树的工作原理。

我们需要二叉树的节点，这将是我们这里的类。 因为我们将创建我们的数据类型，所以我们将把数据点连同左侧和右侧地址一起放置。

我们还没有这样的数据类型，所以我们将按照我们需要的方式创建我们的数据类型。 所以，首先，我们将创建一个类。

现在，我们将为该类创建一个构造函数。 并在必要时在类中传递构造函数。

我们还会给出参数data，将树的数据存储在里面。

我们将使用 self 将数据放入数据参数中。

因为没有数据，就不可能创建节点。 如果我们没有数据，我们将如何处理节点？

如果我们没有数据，我们将没有左和右。 从逻辑上讲，我们需要数据，这就是我们在这里使用数据的原因。

现在我们需要一个节点。

1. 左节点
2. 右节点

我们将在下面的代码中实现它。

我们现在已经实现了二叉树（在下面的代码中）。 我们已经创建了左右节点并将它们设置为 None。

因为在制作节点时，它们应该类似于None。 由于树从根开始，没有左右数据； 我们稍后会添加数据。

现在我们将为树创建一些对象。 要为类 binaryTreeNode 创建对象，我们必须创建一个变量并将其分配给类 binaryTreeNode()。

我们已经为我们的类 binaryTreeNode 创建了三个对象，但是这些对象目前没有与任何东西相关联。 因此，如果我们打印任何对象以查看它包含什么，我们将遵循下面提到的代码。

现在我们将为根的左侧和右侧提供数据点，因为我们已经创建了三个对象 bnt1、bnt2 和 bnt3。 我们认为 bnt1 是根，bnt2 和 bnt3 是 bnt1 的左右。

在这种情况下，我们的二叉树如下所示。 这就是代码的输出方式。

       1
      / \
    /    \
  2       3

这里的根是1，左边是2，右边是3。现在我们用Python打印出来看看效果如何。

我们只想在获得根后打印整棵树。 为此，我们必须定义一个方法。

我们所要做的就是在此处复制该代码并在其中编写新代码。 因为它是二叉树的一部分，所以我们必须用已经写好的代码来写新的代码。

示例代码：

class binaryTreeNode():
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
    def printTree(root):
        print(root.data)
        print('L', root.left.data, end=": ")
        print('R', root.right.data, end=": ")
bnt1= binaryTreeNode(1)
bnt2= binaryTreeNode(2)
bnt3= binaryTreeNode(3)
bnt1.left = bnt2
bnt1.right = bnt3
bnt2.left = bnt1
bnt2.right = bnt3
bnt3.left = bnt1
bnt3.right = bnt2

def printTree(root) 方法为我们提供了根。 因为当我们有树的根时，我们可以访问带有节点的整棵树。

声明方法后，我们将检查一些条件。 我们可以在上面的代码中看到 def PrintTree(root) 方法。

让我们尝试打印 root 1，bnt1，看看我们得到了什么。

示例代码：

print(bnt1.printTree())

输出:

1
L 2: R 3: None

输出显示树包含两个节点（左节点和右节点）。 左边节点的数据是2，右边节点的数据是3。

我们还可以打印 bnt2 和 bnt3 以查看它们包含哪些数据点。

使用 Python 打印整个二叉树

这是整个二叉树。 我们可以运行它并了解有关如何使用 Python 和 Python 的随机库打印二叉树的更多信息。

class BinaryTree:
    def __init__(self, key):
        self.key = key
        self.right = None
        self.left = None
    def insert(self, key):
        if self.key == key:
            return
        elif self.key < key:
            if self.right is None:
                self.right = BinaryTree(key)
            else:
                self.right.insert(key)
        else: # self.key > key
            if self.left is None:
                self.left = BinaryTree(key)
            else:
                self.left.insert(key)
    def display(self):
        lines, *_ = self._display_aux()
        for line in lines:
            print(line)
    def _display_aux(self):
        """Returns list of strings, width, height, and horizontal coordinate of the root."""
        # No child.
        if self.right is None and self.left is None:
            line = '%s' % self.key
            width = len(line)
            height = 1
            middle = width // 2
            return [line], width, height, middle
        # Only left child.
        if self.right is None:
            lines, n, p, x = self.left._display_aux()
            s = '%s' % self.key
            u = len(s)
            first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s
            second_line = x * ' ' + '/' + (n - x - 1 + u) * ' '
            shifted_lines = [line + u * ' ' for line in lines]
            return [first_line, second_line] + shifted_lines, n + u, p + 2, n + u // 2
        # Only right child.
        if self.left is None:
            lines, n, p, x = self.right._display_aux()
            s = '%s' % self.key
            u = len(s)
            first_line = s + x * '_' + (n - x) * ' '
            second_line = (u + x) * ' ' + '\\' + (n - x - 1) * ' '
            shifted_lines = [u * ' ' + line for line in lines]
            return [first_line, second_line] + shifted_lines, n + u, p + 2, u // 2
        # Two children.
        left, n, p, x = self.left._display_aux()
        right, m, q, y = self.right._display_aux()
        s = '%s' % self.key
        u = len(s)
        first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s + y * '_' + (m - y) * ' '
        second_line = x * ' ' + '/' + (n - x - 1 + u + y) * ' ' + '\\' + (m - y - 1) * ' '
        if p < q:
            left += [n * ' '] * (q - p)
        elif q < p:
            right += [m * ' '] * (p - q)
        zipped_lines = zip(left, right)
        lines = [first_line, second_line] + [a + u * ' ' + b for a, b in zipped_lines]
        return lines, n + m + u, max(p, q) + 2, n + u // 2
import random
b = BinaryTree(100)
for _ in range(100):
    b.insert(random.randint(50, 150))
b.display()

输出:

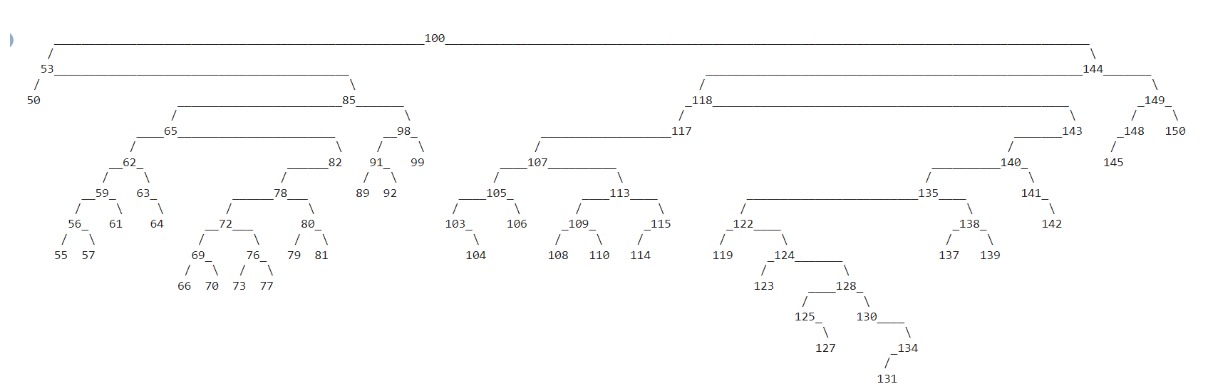
每次运行时，代码的输出都会不断变化。 这是因为我们使用的是 Python 的随机模块。

我们希望您发现本文有助于理解如何使用 Python 打印二叉树。