迹忆客 专注技术分享

树是一种非线性数据结构，其中元素排列在多个级别。 堆是一种基于树的数据结构。

它是一棵完全二叉树，即每个父节点都有两个子节点。 堆实现不同的算法，对其他结构进行排序，对队列进行优先排序等。

堆有两种类型 - 最大和最小。 这些基于子节点与父节点相比的值。

本篇文章将介绍最小堆及其在 Python 中的实现。

Python 中的最小堆

每个父节点都小于或等于最小堆中的子节点。 它遵循升序，优先级总是与较小的节点。

对于给定的节点 n，其左子节点位于 2n+1，右子节点位于 2n+2。

请参见下图。

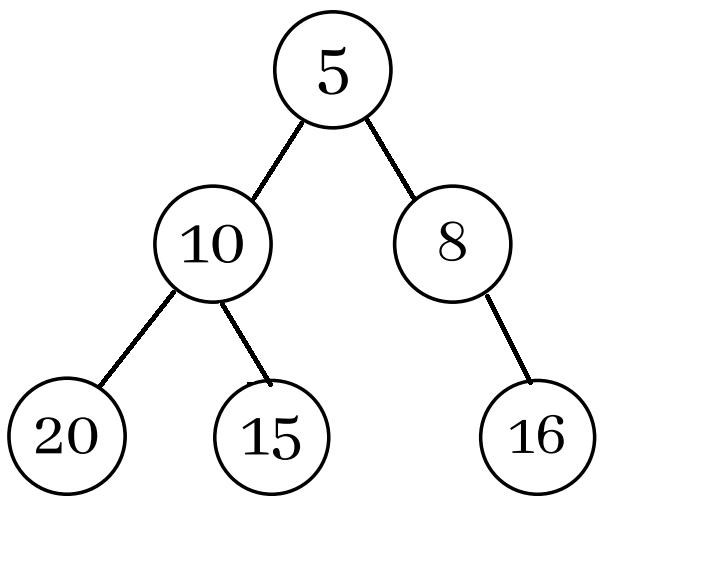
在 Python 中，最小堆可以通过两种方式实现。 这些将在下面讨论。

在 Python 中创建一个类来实现最小堆

我们可以创建一个类来实现 Python 中的最小堆。 我们将用堆的大小初始化类对象，并定义方法来执行元素的插入过程并将它们映射到各自的索引。

例子：

import sys
class min_heap:
    def __init__(self, size):
        self.storage=[0]*size
        self.size = size
        self.heap_size = 0
        self.Heap = [0]*(self.size + 1)
        self.Heap[0] = sys.maxsize * -1
        self.parent = 1
        self.root=1
    def parent_idx(self,idx):
        return (idx-1)//2
    def lf_child_idx(self,idx):
        return 2*idx+1
    def rt_child_idx(self,idx):
        return 2*idx+2
    def has_parent(self,idx):
        return self.parent_idx(idx)>=0
    def insert(self,idx):
        if self.heap_size >= self.size :
            return
        self.heap_size+= 1
        self.Heap[self.heap_size] = idx
        heap = self.heap_size
        while self.Heap[heap] < self.Heap[heap//2]:
            self.swap(heap, heap//2)
            heap = heap//2
    def swap(self, left, right):
        self.Heap[left], self.Heap[right] = self.Heap[right], self.Heap[left]
    def print_heap(self):
        for i in range(1, (self.heap_size//2)+1):
            print("Parent:",str(self.Heap[i]),"Lt: "+str(self.Heap[2 * i]),"Rt: ",str(self.Heap[2 * i + 1]))

min_heap = min_heap(10)
min_heap.insert(5)
min_heap.insert(1)
min_heap.insert(8)
min_heap.insert(2)
min_heap.insert(3)
min_heap.insert(7)
min_heap.insert(9)
min_heap.insert(6)
min_heap.insert(10)
min_heap.print_heap()

输出:

Parent: 1 Lt: 2 Rt:  7
Parent: 2 Lt: 5 Rt:  3
Parent: 7 Lt: 8 Rt:  9
Parent: 5 Lt: 6 Rt:  10

insert() 方法将元素添加到堆中。 使用 swap() 方法管理元素的索引和顺序，该方法使用 rt_child_index() 和 lt_child_index() 函数根据父节点的值调整子节点的级别。

使用类的 print_heap() 函数迭代最小堆并按顺序显示。

使用 heapq 模块在 Python 中实现最小堆

Python提供了一个heapq模块，可以在不创建其他类的情况下实现堆数据结构。 该模块确保每次弹出堆的最小元素以保持最小堆结构。

我们将使用一个列表来维护堆的节点。 使用 heappush() 函数添加元素，并相应地维护顺序，以便维护 Min Heap 的结构。

heappop() 从堆中弹出最小的元素，即根节点。

例子：

import heapq as heap
lst=[ ]
heap.heappush(lst,7)
heap.heappush(lst,1)
heap.heappush(lst,5)
heap.heappush(lst,4)
heap.heappush(lst,8)
heap.heappush(lst,3)
print("Heap: ",lst)
print("Parent Node: ",heap.heappop(lst))
print("Child Nodes: ",lst)

输出:

Heap:  [1, 4, 3, 7, 8, 5]
Parent Node:  1
Child Nodes:  [3, 4, 5, 7, 8]

在上面的例子中，我们使用了一个列表 lst 来维护堆。 添加元素，并使用 heappush() 函数自动调整它们的顺序。

显示最小堆。 使用 heappop() 方法弹出父节点并显示。

移除父节点后，剩余的子节点也会显示出来。