Python 音频合成

当前位置：主页 > 学无止境 > 编程语言 > Python >

Python PHP Java Go TypeScript C++ Vba Node.js C语言 MATLAB

Python 音频合成

作者：迹忆客最近更新：2023/04/23 浏览次数：

今天，我们将学习音频合成以及如何使用 Python 生成声音。

Python 音频合成

声音合成或音频合成以电子方式（使用硬件或软件）生成模仿人声或乐器的声音。

合成主要用于音乐，其中称为合成器的电子设备/乐器用于录制和演奏音乐。

现在，关键是我们可以使用 Python 来生成这些简单的声音，例如正弦波吗？我们是否有任何模块，或者我们如何创建自己的模块？

让我们学习下面的不同方法。

在 Python 中使用 IPython.display 进行加法合成

首先，我们导入必要的模块和库。我们导入 IPython 来显示声音播放器，导入 numpy 来处理数组，导入 matplotlib 来绘制图表（我们将在生成基本波形的同时进行），导入数学来使用数学函数。
```
import IPython.display as ipd
import numpy
import math
import matplotlib.pyplot as plt
```
设置采样率。在这里，我们将 sample_rate 设置为 22050。
```
sample_rate = 22050
```
制作正弦波。
```
def makesine(frequency, duration):
t = numpy.linspace(0, duration, math.ceil(sample_rate*duration))
x = numpy.sin(2 * numpy.pi * frequency * t)
return x
```
在这一步，我们定义了一个函数makesine()，它以频率和持续时间为参数。我们在 numpy.linspace() 方法中使用持续时间，在 numpy.sin() 方法中使用频率来重用纯正弦波形。

请注意， numpy.linspace() 创建数字序列，或者我们可以说它返回均匀间隔的数字/样本 w.r.t。间隔（开始，停止）。它与 numpy.arange() 类似，但将样本编号 (num) 作为参数而不是步骤。

另一方面，numpy.sin() 计算所有指定 x（元素数组）的三角正弦值。

Run makesine()。

output = numpy.array(())
y = makesine(261.63, .5) # C for 0.5 seconds

output = numpy.concatenate((output, y))
y = makesine(293.66, .5) # D for 0.5 seconds

output = numpy.concatenate((output, y))
y = makesine(329.63, .5) # E for 0.5 seconds

output = numpy.concatenate((output, y))
ipd.Audio(output, rate=sample_rate)

接下来，我们多次执行 makesine() 以形成具有指定频率和持续时间的新波形。之后，我们使用 numpy.concatenate() 将它们放在一起。

您可以在下面找到完整的工作源代码以及相应的输出。

这是完整的源代码。

import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy
import math

sample_rate = 22050

def makesine(frequency, duration):
  t = numpy.linspace(0, duration, math.ceil(sample_rate*duration))
  x = numpy.sin(2 * numpy.pi * frequency * t)
  return x

output = numpy.array(())
y = makesine(261.63, .5) # C for 0.5 seconds

output = numpy.concatenate((output, y))
y = makesine(293.66, .5) # D for 0.5 seconds

output = numpy.concatenate((output, y))
y = makesine(329.63, .5) # E for 0.5 seconds

output = numpy.concatenate((output, y))
ipd.Audio(output, rate=sample_rate)

在 Python 中使用加法合成制作各种基本波形

我们完成了基本的正弦波形。让我们使用 frequency * i 来试验各种频率为整数倍的基本波形；在这里，我是从 1 开始的计数器，每次递增 1。

我们需要将这些正弦波软化为预定义的振幅 (amplist)，然后将其叠加在输出中。为此，我们需要创建一个名为 addsyn() 的函数，如下所示：

def addsyn(frequency, duration, amplist):
    i = 1
    t = numpy.linspace(0, duration, math.ceil(sample_rate*duration))
    output = numpy.zeros(t.size)

    for amp in amplist:
        x = numpy.multiply(makesine(frequency*i, duration), amp)
        output = output + x
        i+=1

    if numpy.max(output)>abs(numpy.min(output)):
        output = output / numpy.max(output)
    else:
        output = output / -numpy.min(output)
    return output

在 addsyn() 内部，我们初始化一个新的输出。在 for 循环中，我们制作具有最大幅度 (amp) 的正弦波；这里，频率是整数倍。

然后，我们将其与输出相加并将其保存在输出变量中。接下来，我们确保最大幅度不超过 1 并返回输出。

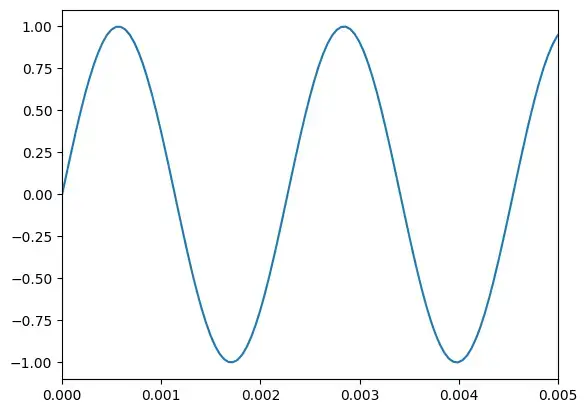
现在，我们可以执行以下代码来制作一个谐波正弦波，并为其制作一张仅显示 0.005 秒的图表以查看此波形。

t = numpy.linspace(0, 1, sample_rate)
sinewave = addsyn(440, 1, [1])
plt.plot(t, sinewave)
plt.xlim(0, 0.005)
ipd.Audio(sinewave, rate=sample_rate)

完整的源代码如下。

import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy
import math

sample_rate = 22050

def addsyn(frequency, duration, amplist):
    i = 1
    t = numpy.linspace(0, duration, math.ceil(sample_rate*duration))
    output = numpy.zeros(t.size)

    for amp in amplist:
        x = numpy.multiply(makesine(frequency*i, duration), amp)
        output = output + x
        i+=1

    if numpy.max(output)>abs(numpy.min(output)):
        output = output / numpy.max(output)
    else:
        output = output / -numpy.min(output)
    return output

t = numpy.linspace(0, 1, sample_rate)
sinewave = addsyn(440, 1, [1])
plt.plot(t, sinewave)
plt.xlim(0, 0.005)
ipd.Audio(sinewave, rate=sample_rate)

输出:

python音频合成——基本的正弦波谐波图

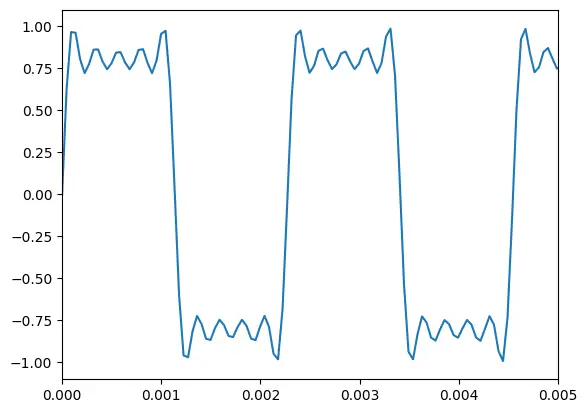
现在，我们可以尝试使用 addsyn() 函数的不同值来获得不同的输出。请参阅下面创建方波的另一个示例。

示例代码：

import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy
import math

sample_rate = 22050

def addsyn(frequency, duration, amplist):
    i = 1
    t = numpy.linspace(0, duration, math.ceil(sample_rate*duration))
    output = numpy.zeros(t.size)

    for amp in amplist:
        x = numpy.multiply(makesine(frequency*i, duration), amp)
        output = output + x
        i+=1

    if numpy.max(output)>abs(numpy.min(output)):
        output = output / numpy.max(output)
    else:
        output = output / -numpy.min(output)
    return output

t = numpy.linspace(0, 1, sample_rate)
square_wave = addsyn(440, 1, [1, 0, 0.349, 0, 0.214, 0, 0.156, 0, 0.121, 0])
plt.plot(t, square_wave)
plt.xlim(0, 0.005)
ipd.Audio(square_wave, rate=sample_rate)

输出:

python音频合成——基本的正弦波方图

在 Python 中使用 pyaudio 生成音频合成

在这里，我们将使用 pyaudio，一个用 Python 录制音频的 Python 模块。

首先，我们导入必要的库：用于执行数学函数的 math 和用于生成波的 pyaudio。

import math        #import needed modules
import pyaudio     #sudo apt-get install python-pyaudio

初始化pyaudio。
```
PyAudio = pyaudio.PyAudio
```
初始化变量。
```
bit_rate = 16000
frequency = 500
length = 1

bit_rate = max(bit_rate, frequency+100)
number_of_frames = int(bit_rate * length)
rest_frames = number_of_frames % bit_rate
wave_data = ''
```
在这里，我们将 bit_rate 初始化为 16000，它显示每秒的帧数。频率设置为 500 Hz，表示每秒的波数（261.63=C4-note），而长度初始化为 1。

之后，我们使用 max() 函数从 bit_rate 和 frequency+100 中找到最大值，并将最大值赋给 bit_rate。然后，我们将 bit_rate 和 length 相乘，使用 int() 函数将其转换为 int 类型并将其分配给 number_of_frames。

接下来，我们使用取模运算符 (%) 将 number_of_frames 除以 bit_rate，并将余数分配给 rest_frames。最后，我们用空字符串初始化 wave_data。

产生波浪。

for x in range(number_of_frames):
  wave_data = wave_data+chr(int(math.sin(x/((bit_rate/frequency)/math.pi))*127+128))

for x in range(rest_frames):
  wave_data = wave_data+chr(128)

在这里，我们使用了两个 for 循环，循环迭代直到 number_of_frames 生成波。

录制音频。
```
p = PyAudio()
stream = p.open(format = p.get_format_from_width(1),
            channels = 1,
            rate = bit_rate,
            output = True)
stream.write(wave_data)
stream.stop_stream()
stream.close()
p.terminate()
```
在这里，我们创建了一个 PyAudio 实例，将引用保存在 p 中，并使用该引用使用 open() 方法打开流，这将记录音频。接下来，我们编写 wave_data，停止并关闭流。最后，也终止 PyAudio 实例 (p)。

这是完整的源代码。

import math
import pyaudio

PyAudio = pyaudio.PyAudio

bit_rate = 16000
frequency = 500
length = 1

bit_rate = max(bit_rate, frequency+100)
number_of_frames = int(bit_rate * length)
rest_frames = number_of_frames % bit_rate
wave_data = ''

for x in range(number_of_frames):
  wave_data = wave_data+chr(int(math.sin(x/((bit_rate/frequency)/math.pi))*127+128))

for x in range(rest_frames):
  wave_data = wave_data+chr(128)

p = PyAudio()
stream = p.open(format = p.get_format_from_width(1),
              channels = 1,
              rate = bit_rate,
              output = True)

stream.write(wave_data)
stream.stop_stream()
stream.close()
p.terminate()