迹忆客 专注技术分享

嘿 Java 程序员，如果你想在 Java 中实现二分搜索，并寻找迭代和递归二分搜索算法，那么你来对地方了。 今天要教大家一个重要的算法。 在计算机科学中，二分搜索或半区间搜索是一种分而治之的算法，它定位一个项目在排序数组中的位置。 二分搜索通过将输入值与数组的中间元素进行比较来工作。 比较确定元素是否等于输入、小于输入或大于输入。

当被比较的元素等于输入时，搜索停止并通常返回元素的位置。 如果元素不等于输入，则进行比较以确定输入是小于还是大于元素。

根据它是什么算法然后重新开始但只搜索数组元素的顶部或底部子集。 如果输入不在数组中，算法通常会输出一个唯一值来指示这一点。

二分搜索算法通常在每次连续迭代中将要检查的项目数量减半，从而在对数时间内定位给定项目（或确定其不存在）。

二分查找是一种分而治之的查找算法。 它的工作原理是将输入集分成两半，然后应用算法并重复相同的步骤，直到工作完成。

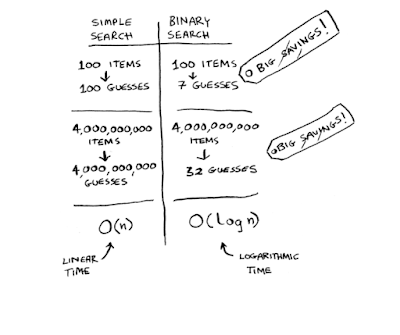
没有递归的 Java 二分搜索它也非常直观，充满了有用的图表，很好地解释了这些概念。 例如，在上图中，我们可以看到当元素数量增加时，线性搜索变得越来越慢，但二分搜索却没有。 例如，对于 40 亿个项目，二分查找只需要 32 个猜测

没有递归的 Java 中的二分搜索示例

该算法是递归实现的。 此外，关于 Java 中二分搜索实现的一个有趣事实是，著名的 Effective Java 书籍的作者 Joshua Bloch 在 java.util.Arrays 中实现了二分搜索。

import java.util.Arrays;

/**
 * 实现二进制搜索的 Java 程序。
 */
public class Main {
    public static void main(String args[]) {
        int[] list = new int[]{23, 43, 31, 12};
        int number = 12;
        Arrays.sort(list);
        System.out.printf("Binary Search %d in integer array %s %n", number, Arrays.toString(list));
        binarySearch(list, 12);
        System.out.printf("Binary Search %d in integer array %s %n", 43, Arrays.toString(list));
        binarySearch(list, 43);
        list = new int[]{123, 243, 331, 1298};
        number = 331;
        Arrays.sort(list);
        System.out.printf("Binary Search %d in integer array %s %n", number, Arrays.toString(list));
        binarySearch(list, 331);
        System.out.printf("Binary Search %d in integer array %s %n", 331, Arrays.toString(list));
        binarySearch(list, 1333);
        Arrays.sort(list);
        int index = Arrays.binarySearch(list, 3);
    }

    /**
     * 在 Java 中的排序数组中执行二分搜索
     * @param input
     * @param number
     * @return 元素在数组中的位置
     */
    public static void binarySearch(int[] input, int number) {
        int first = 0;
        int last = input.length - 1;
        int middle = (first + last) / 2;
        while (first <= last) {
            if ( input[middle] < number){
                first = middle + 1;
            } else if (input[middle] == number) {
                System.out.printf(number + " found at location %d %n", middle);
                break;
            } else {
                last = middle - 1;
            }
            middle = (first + last) / 2;
        } if ( first > last){
            System.out.println(number + " is not present in the list.\n");
        }
    }
}

执行结果如下

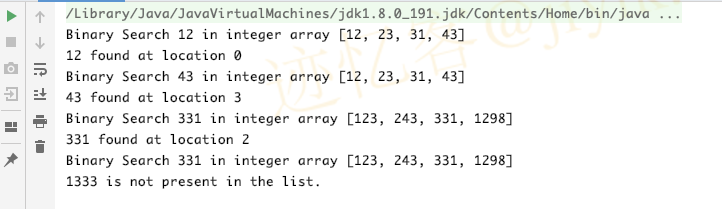
这就是关于如何在没有递归的情况下在 Java 中实现二进制搜索算法的全部内容。 与任何递归算法一样，此代码不使用任何循环，如 while 、for 或 do-while 循环。 理想情况下，我们不需要为日常任务的二分搜索编写代码，因为 Java 库已经有一个 binarySearch() 方法，但了解如何编写这些算法有助于面试。