JIYIK CN >

In a distributed system, a core issue is data consistency. Therefore, the consistency algorithm is of utmost importance in a distributed system. The Paxos algorithm is designed to solve the consistency problem, but it has always been considered difficult to understand, probably because it is described in ordinary language, so it is difficult for readers to understand. If you want to understand the Paxos algorithm, it is recommended to read the "original book" - "Paxos Made Simple" first.

Okay, without further ado, let’s enter the world of Paxos.

Problem

Assuming that a group of programs want to submit some values, how can we ensure the uniqueness of these values? The consistency algorithm is to ensure that only one value is selected among these values. Of course, if a value is selected, then these programs should be able to obtain this selected value.

Therefore, we can see that there should be three roles in this process - proposers, acceptors and learners. In the process of implementing this algorithm, a member may have to play multiple roles.

The simplest way to select a worthwhile candidate is to have only one acceptor in each group, and a proposer submits a proposal to this acceptor, which selects the first proposal it receives. Although this method is simple, it does not meet our requirements. Because once the acceptor has a problem, the program will not be able to continue.

Therefore, we need to use other methods to select this value. Instead of using a single acceptor, we use multiple acceptors to complete this process. That is to say, the proposer changes from submitting proposals to one acceptor to submitting proposals to a group of acceptors. An acceptor will approve a proposal. When the value of a proposal is approved by all acceptors in a large enough group, the proposal is said to be selected. Then the question is, how large is a large enough group [Q1] ?

For Q1, we can understand it this way: for all acceptors, there is a set {acceptor1, acceptor2, acceptor3, .., acceptor(n)} A. Suppose there is a set T, each element in T is a group of acceptors. These groups in T are composed of acceptors in A.

T: {{acceptor(k),acceptor(k+1), ...,acceptor(j)}, {acceptor1,acceptor2,...,acceptor(m)}, ..., {acceptor(l),acceptor(l+1),...,acceptor(n)}}

For any two sets of acceptors in T, there is at least one common acceptor. Such a set T can be considered large enough, that is, a large enough group proposed in Q1.

OK, now that we know that the group is large enough, we can move on. Because any two groups have at least one common acceptor, a proposal can only be selected if an acceptor approves at most one proposal. It should be noted here that an acceptor can only approve at most one proposal during an election. When the next election is held, the acceptor is allowed to approve the proposal again. At this point, you may be a little confused about this issue. It doesn't matter, please continue reading. Once you understand the following questions, you will suddenly understand them when you come back here.

In the absence of information loss, even if only one proposer submits a proposal, we hope that the proposal will be selected. This leads to the first condition in the Paxos algorithm:

P1. An acceptor must approve the first proposal it receives.

In the original book it says:

P1. An acceptor must accept the first proposal that it recevies.

My translation here should be correct.

However, we see that the requirement of P1 should cause such a problem. When multiple proposers submit multiple different proposals at the same time, it is possible that no proposal will be approved by more than a majority of acceptors [Q2] . How should we understand this problem? Under the requirement of P1, each acceptor must approve the first proposal it receives. So the following scenario will occur:

The proposals received by multiple acceptors are different

That is, acceptor 1 receives value1 first, acceptor 2 receives value2 first, and so on. They all approve the first proposal they receive, which leads to the problem in Q2. Even if only two proposals are proposed and each proposal is approved by almost half of the acceptors, even if only one acceptor fails, there is no way to guarantee that a proposal will be selected under P1's requirements.

We know that the premise for a proposal to be selected is that the proposal is approved by more than half of the acceptors. And P1 stipulates that an acceptor must approve the first proposal it receives, so the P1 condition gives rise to the question Q2 we explained above. So based on the above situation, we can deduce that an acceptor must be allowed to receive multiple proposals. The acceptor will assign a serial number to each proposal. So at this point our proposal has been changed. It is no longer composed of only value. The current proposal consists of two parts: number and value. At the same time, it is required that the numbers between any two proposals are different. So far, we have two more weapons:

1. An acceptor can receive multiple proposals.

2. Each proposal consists of two parts: a number and a value. The numbers of any two proposals are different.

Let's take up our weapons and move on. There are two conclusions that need to be explained.

In order for a proposal to be selected, it must be approved by more than half of the acceptors; we allow multiple proposals to be selected in another election, but the values ​​of these selected proposals must be the same. It seems that there is a glimmer of hope here. The proposals have been numbered, which is of great help to our subsequent arguments. In the algorithm, as long as the following conditions are met, we can ensure the uniqueness of the selected proposal:

P2: If a proposal with v is selected, assuming that the proposal number is m, then the value of any selected proposal greater than m is v.

Similarly, P2 said this in the original book:

P2: If a proposal with value v is chosen, then every higher-numbered proposal that is chosen has value v.

Because the numbers are in order, if P2 is guaranteed to be true, our initial requirement can be met.

不过看了P2就感觉先前看到的那一丝光明又消失了。且看P1是要每个acceptor批准其接收到的第一个提案。而到了P2则讨论的就直接是对于选中的提案的要求。从P1到P2这期间究竟发生了什么，我们不得而知。不过没关系，毕竟我们从P2中可以知道，只要满足了P2就能满足只有一个值被选中的这一关键点——这也是我们所希望达到的目的。

下面我们来做的就是反推应该如何来保证P2能够成立。说到这是不是刚才感觉要消失的那一丝光明又在眼前重现了。

那P2又该如何来满足呢？首先，一个提案要想被选中，那该提案必须被至少一个acceptor所批准。这一点是毋庸置疑的。因此，新的条件又产生了。

P2a：如果一个值为v的提案被选中了，假设编号为m。那么对于每个编号大于m的提案来说，如果被acceptor批准，该提案的值也必须为v。

该条件在原著中是这样说的

P2a: If a proposal whth value v is chosen, then every heigher-numbered proposal accepted by any acceptor has value v.

经过P2a，貌似P2可以得到满足了。因为提案的编号是全序的，也就是说后提交的提案的编号肯定是大于先提交的提案的编号了。而对于P2a条件中的要求，后提交的并且被批准的提案其值必须为v。这样P2肯定会被满足了。

所以说只要满足P2a就能满足P2从而我们最初的目的也能达到，至少目前是这样的。但是，我们再回过头来看P1，就会发现，其实还有一些地方是我们遗漏的。我们知道，成员之间的通信是异步的。假如有一个acceptor，暂称其为C，还未收到任何提案的时候有一个编号为m的提案就已经被选中了。假设这时一个新的proposer被唤醒，然后提交了一个编号大于m的提案，并且该提案的值和m也不相同。当C收到这个提案以后，根据P1，C是必须要批准这个提案的。这时就违背了P2a了。对于P2a，我们能看出，是站在acceptor角度提出的。因此就产生了上面的问题。所以需要再次站在proposer的角度来提出一些限制。

P2b： 一个值为v的提案被选定了，该提案编号为m。那么对于任何编号大于m的由proposer提交的提案的值必须为v。

同样我们引用原文

P2b: If a proposal with value v is chosen, then every higher-numbered proposal issued by any proposer has value v.

由于一个提案在被acceptor批准之前必须由提议者提交，因此P2b可以满足P2a从而满足了P2。在这里，站在proposer的角度提出了P2b。那又该如何来保证P2b呢？我们假设某个编号为m，值为v的提案被选中了，对于任何被提出的编号为 n（n > m）的提案，其值都为v。现在我们使用归纳法来证明该说法是成立的。

提案[ m , v ]被选中，我们的假设条件如下

对于编号在 m...(n-1) 中的任何一个被提出的提案的值都为v。

同时由于提案m被选中，因此肯定有一个集合C，包含半数以上的acceptor，C中的每一个acceptor都批准了提案m。因此我们可以推断出，在C中的每一个acceptor都批准了编号在m...(n-1)范围内的一个提案，并且m...(n-1)中的被任意一个acceptor批准的提案的值都为v（这里需要注意的是，任意一个acceptor并不都是值得C中的acceptor）。

由于任意一个集合S，包含了半数以上的acceptor，肯定会至少包含一个C中的acceptor，所以我们可以通过下面的条件来满足P2b。也就是任意一个被提出的编号为n (n > m)的提案的值都为v。

P2c：对于任意的v和n，如果一个编号为n，值为v的提案被提出的话，肯定存在一个包含半数以上的acceptor的集合S满足：要么集合S中没有一个acceptor批准过任意的编号小于n的提案；要么对于集合S中批准的编号小于n的那些提案中，编号最大的提案的值为v。

通过保持P2c的不变性，就能保证P2b。从而满足P2a，进而满足P2。最终满足我们最初的要求。

同样的，问题又来了。既然由P2c => P2b => P2a => P2。那我们又由什么来证明P2c的完整性呢[Q3]？

对于Q3，我们可以使用反证法来证明。

假设提案[m,v]已经被选定，有提案n ① n=m+1 假设n的值不为v，而为w。则根据P2c要么有一组S从来没有批准过小于n的提案；要么在批准的所有编号小于n的提案中，编号最大的提案的值为w。因为S和C至少有一个公共acceptor，所以说两个条件都不满足。所以假设不成立。因此n的值为v。② 编号m属于m...(n-1)，假设n的值不为v，设为w’ 。则存在一个集合S’，要么在S’中没有一个acceptor批准过编号小于n的提案；要么在S’中批准过的所有的编号小于n的提案中，编号最大的提案的值为w’，设该提案的编号为p(p∈m...(n-1))。根据我们在归纳法中的假设条件编号属于m...(n-1)的提案的值都为v，并且S’和C至少有一个公共acceptor，所以由S’中的acceptor批准的小于n的提案中编号最大的那个提案也属于m...(n-1)。从而可以推导出w’=v。即可证明提案n的值为v。

到这里我们就证明了P2C的完整性。

由此可见，一个proposer要想提交一个编号为n的提案，首先获取到编号小于n的那些提案中编号最大的那个提案，假设该提案编号为p，如果有这个提案的话，提案p已经或者将要被某一个包含半数以上的acceptor的集合中的所有的acceptor所批准。获取这样的一个已经被批准的提案是非常简单的，相反预测一个批准的提案是非常困难的。所以，一个proposer可以请求acceptor不要批准任何小于编号n的提案。这时，核心的算法就要产生了：

1. 一个proposer准备提交一个编号为n的提案之前，首先会向某组（含半数以上的acceptor）中的每个成员发出请求，希望得到如下的响应：
    a. Acceptor承诺不再批准任何编号小于n的提案。
    b. 如果acceptor批准过小于编号n的提案，则将编号最大的提案响应给proposer。

我们称这个请求过程为提案n的prepare请求。

2. 如果proposer从某个组（包含半数以上的acceptor）中的acceptor方面得到响应，那么该proposer就可以提交值为v的提案n了。当然了，这里的v要视响应消息而定。如果得到的响应是acceptor已经批准的编号小于n的的那些提案中的编号最大的提案，那么提案n的值v就是响应的提案的值；如果得到的响应消息是acceptor没有批准过任何编号小于n的提案，那么值v就可以是任意的了。得到prepare请求的响应以后，proposer再次向同一

acceptor发出批准该提案的请求。我们称其为accept请求。

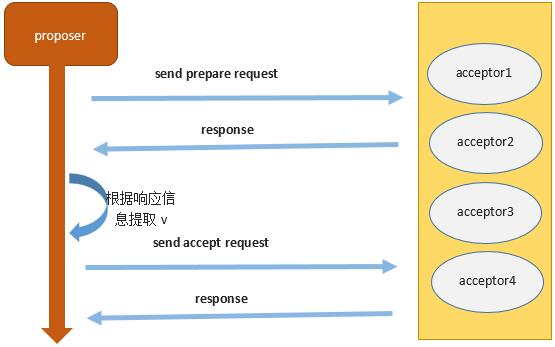
上面的算法是对proposer提出的。那对于acceptor方面有该如何处理呢？在上面的过程中，acceptor会收到两种类型的请求：prepare和accept。

acceptor是可以忽略任何请求的，并且不用考虑是否能满足什么条件。 所以说，这里我们说的是acceptor会对一个请求进行响应的情况。acceptor对于prepare 请求总是会积极响应。对于accept请求，如果他没有响应过不去批准该提案，那它会响应一个批准该提案的消息。也就是下面的条件

P1a：acceptor对于编号为n的提案的accept请求，如果之前没有对编号大于n的提案的prepare请求进行过响应，那么该acceptor会批准编号为n的提案。

原著中是这样描述的

P1a. An acceptor can accept a proposal numbered n iff it has not responded to a prepare request having a number greater than n.

我们看，在P1a中是包含P1的。

到目前为止我们已经有了一个比较完整的算法。现在我们将proposer和acceptor综合起来，看一下整个算法的过程。

Phase1 （a）proposer选择一个编号为n的提案，并且发送一个带有编号n的prepare请求给一组包含半数以上的acceptor。
（b）一个acceptor接收到一个关于编号n的prepare请求，发现编号n比其先前接收到的所有的提案的编号都大，并且对于这些提案的prepare请求都已经进行了响应。那么acceptor会向n的prepare请求回应的消息包括两部分：一是，不会再批准任何小于n的提案；二是，将已经批准的编号小于n的的那些提案中的编号最大的提案的值，当然这个提案要存在。如果不存在则仅仅响应第一条。

Phase2 （a）当proposer从包含半数以上的一组acceptor那里收到关于编号n的提案的prepare请求的响应信息，那么它将会向这组acceptor发送一个编号为n值为v的提案的accept请求。这个v的值根据proposer得到的响应信息来定：如果在响应信息中包含有提案信息，那这个v就是该提案的值；如果没有提案信息，则v可以是任意值，只要proposer愿意。
（b）如果acceptor收到一个关于n的提案的accept请求，除非acceptor已经向大于n的提案的prepare请求进行了响应，否则该acceptor是会批准编号为n的提案的。

一个proposer只要遵循上面的步骤，他就可以生成多个提案。在上面的过程中，proposer可以在任意的时刻终止一个提案。对于acceptor来说，无论如何，如果acceptor由于之前已经向一个编号更大的提案的prepare请求进行了响应而要忽略当前提案的prepare或者accept请求的话，必须要能通知到proposer。由proposer来放弃这个提案的提交。

上面就是关于proposer和acceptor的算法。说到这里，对于proposer和acceptor要做的事情就已经清楚了。但是我们知道，在Paxos算法中是存在三种角色的。除了proposer和acceptor以外还有learner。既然我们的提案已经选出来了，那就需要learner来学习了。下面我们就来看一下learner是如何学习一个已经被选中的提案的。

最简单的方式就是，learner必须获取被半数以上acceptor批准的提案。所以，必须使每个acceptor，不论何时只要它批准一个提案就会通知到所有的learner，并将批准的proposal发送给learner。因此，learner可以及时的获取一个被选中的提案。但是，这种方式的代价就是会有大量的通信。因为这种方式要求每个acceptor向每个learner都要发送消息。[方式一]

还有一个方式就是，指定一个特定的learner负责和acceptor进行通信。acceptor只负责将其批准的提案发送给这个特定的learner，由这个learner再将其发送给其他的learner。[方式二]

方式二虽然有效的减少、了通信的次数，但是这种方式却是不可靠的。因为一旦那个特定的learner出现故障，所有的learner都将获取不到提案。所以在方式二的基础上演变出来了方式三。不再指定一个特定的learner，而是指定多个learner负责和acceptor通信，然后再将信息发送给其他的learner。很明显，这种方式较方式二来说通信次数又增加了，但是较方式一，通信次数依然是减少的。而且这种方式是比较可靠的。

考虑到，在实际场景中消息是会丢失的。一个被选中的提案可能不会被learner获取到。这时候它可以向acceptor询问一个其已经批准的提案，但是这个acceptor是没有办法知道这个提案是否被大多数的acceptor所批准。在这种情况下，learner可以求助于proposer。它可以让一个proposer按照之前描述的步骤来提交一个提案。如果该提案被提交成功了，根据之前的P2c、P2b等条件可以知道该提案的值已经被选中；否则该值没有被选中。

算法到这里就已经完整了。对于开始说到的三个角色——proposer、acceptor和learner，各自要进行的动作都已经明确了。下面来说一个比较特殊的情况。

我们来假设这样的一个情景：有两个proposer——p和q，每一个都会提出一系列编号递增的提案。这些提案都没有别选中过。现在p完成了阶段1的编号为n1的提案。然后p完成了阶段1的编号为n2（n2 > n1）的提案。所以对于n1的阶段2的accept请求会被忽略，因为所有的acceptor都已经向n2的prepare响应了不会再批准任何编号小于n2的提案。因此，p开始提出n3（n3 > n2），并且完成了prepare的请求。同样，这时n2的accept请求也会被忽略。以此进行下去岂不是就成了一个死循环了。

为了解决这个问题，参照learner学习提案的方式二，指定一个特定的proposer，使其作为唯一的可以提出提案的proposer。

所有上面的算法都有一个前提，就是任何两个proposer提出的提案的编号都不相同。

上面一堆堆的文字可能有些啰嗦，多数都是参照原文翻译过来的。有不确切的地方还希望多多指教！

参考文献：《Paxos Made Simple》